Question

A photon of energy $h \nu$ and momentum $\dfrac{h \nu}{c}$ collides with an electron at rest. After the collision, the scattered electron and the scattered photon each make an angle of $45^{\circ}$ with the initial direction of motion. The ratio of frequency of scattered and incident photon is:
a) $\sqrt{2}$
b) $\sqrt{2} - 1$
c) $2$
d) $\dfrac{1}{\sqrt{2}}$

Answer 1

The collision between two particles—a photon and an electron at rest where momentum and energy are conserved in the phenomena called Compton’s effect. In this collision, the horizontal component needs to be balanced for finding the ratio of frequency of scattered and incident photons as vertical momentum is the same for both.

Complete step by step answer:
Let the frequency of scattered photons be $\nu^{‘}$.
Apply conservation of momentum in vertical direction,
The momentum of scattered electrons and photons are the same and equal to $\dfrac{h \nu}{c}$.

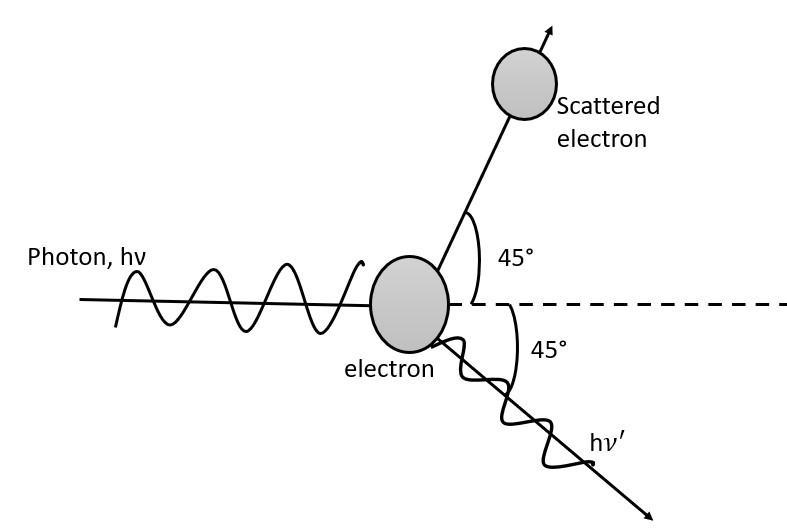
Apply conservation of momentum in horizontal direction,
$\dfrac{h \nu}{c} =2 \dfrac{h \nu^{‘}}{c} cos \theta$
Here, $\theta = 45^{\circ}$ the angle of scattered photons and scattered electrons with the horizontal.
$\nu = 2 \nu^{‘} cos 45^{\circ}$
$\dfrac{ \nu^{‘}}{\nu} = \dfrac{1}{2 cos 45^{\circ}}= \dfrac{\sqrt{2}}{2}$
$\dfrac{ \nu^{‘}}{\nu}= \dfrac{1}{\sqrt{2}}$

So, the correct answer is “Option d”.

Note: Photon with energy and momentum collides with the electron at rest. After a collision, some of the momentum and energy is transferred to the electron. Electrons have attained kinetic energy. Energy and momentum are conserved in this as it is an elastic collision.