Question
Question: A person’s eye level is \(1.5\,m\). He stands in front of a \(0.3\,m\) long plane mirror which is \(...
A person’s eye level is 1.5m. He stands in front of a 0.3m long plane mirror which is 0.8m above the ground. The height of the image he sees of himself is:
(A) 1.5m
(B) 1.0m
(C) 0.8m
(D) 0.6m
Solution
Hint The height of the image he sees of himself is determined by using the law of the reflection. The object which creates the image behind the mirror at the same distance that it has from the mirror in front of it. The properties of the triangle are also required to solve this problem.
Useful formula:
The property of the triangle is given by the ratio of corresponding lengths are equal, then
ADAB=DEBC
Complete step by step answer
From the given information, thee rough diagram is drawn, then
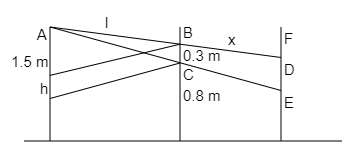
Let us assume that the person is at the point of A, then assume that the two triangles ∠ABC and the triangle ∠ADE then the height is determined. The position of the person is A and the mirror is BC and the image behind the mirror is assumed as the DE, then by using the two triangles which are mentioned in the above statement, the height of the image can be determined.
Now,
The property of the triangle is given by the ratio of corresponding lengths are equal, then
ADAB=DEBC....................(1)
By substituting the values of the terms in the above equation (1) from the diagram, then the above equation (1) is written as,
2ll=h0.3
By cancelling the same terms in the above equation, then the above equation is written as,
21=h0.3
By dividing the terms in the above equation, then the above equation is written as,
0.5=h0.3
By rearranging the terms in the above equation, then the above equation is written as,
h=0.50.3
By dividing the terms in the above equation, then the above equation is written as,
h=0.6m
Hence, the option (D) is the correct answer.
Note: The lengths and the angles of the triangles are noted carefully in the similar triangles. While choosing the similar triangles, the student must choose the exact similar triangle. If the students may choose the different triangles the solution must be wrong.
