Question

A person with a normal near point $\left( {25\,cm} \right)$ using a compound microscope with an objective of focal length $8\,mm$ and an eyepiece of the focal length $2.5\,cm$ can bring an object placed at $9\,mm$ from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope.

Answer 1

Hint- The separation between two lenses will be the sum of the image distance of the objective lens and the object distance of the eyepiece.
The image distance of the objective lens and object distance of eyepiece can be found using the lens formula.
The magnification can be found using the formula $m = \dfrac{{{v_o}}}{{\left| {{u_o}} \right|}}\left( {1 + \dfrac{d}{{{f_e}}}} \right)$
Where, ${v_o}$ is the image distance of objective lens, ${u_o}$ is the object distance of objective lens, $d$ is the distance of near point and ${f_e}$ is the focal length of eyepiece.

Complete step by step answer:
It is given that the focal length of the objective lens is
${f_o} = 8\,mm = 0.8\,cm$
The focal length of the eyepiece is given as
${f_e} = 2.5\,cm$
The distance of the object from the objective lens is given as
${u_o} = 9\,mm = 0.9\,cm$
We need to find the separation between the objective lens and eyepiece.
Let us use the lens formula to find the answer.
The lens formula is given as
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Where, f is the focal length, v is the image distance and u is the object distance.
Now let us substitute the values of the objective lens in this equation.
$\dfrac{1}{{{f_o}}} = \dfrac{1}{{{v_o}}} - \dfrac{1}{{{u_o}}}$

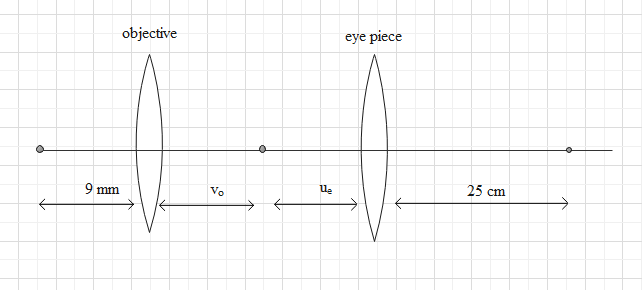
We can take the left side of the objective lens as negative and right side as positive direction. Since object is on the left side, we can take
${u_o} = - 0.9\,cm$
Thus, we get
$\dfrac{1}{{0.8}} = \dfrac{1}{{{v_o}}} - \dfrac{1}{{ - 0.9}}$
$\Rightarrow \dfrac{1}{{0.8}} - \dfrac{1}{{0.9}} = \dfrac{1}{{{v_o}}}$
$\therefore {v_o} = 7.2\,cm$
Now let us use the lens formula in the eyepiece.
$\dfrac{1}{{{f_e}}} = \dfrac{1}{{{v_e}}} - \dfrac{1}{{{u_e}}}$
The near point is given as,
$d = 25\,cm$
This will be the image distance of the eye piece.
Thus,
${v_e} = 25\,cm$
On substituting the values, we get
$\Rightarrow \dfrac{1}{{{u_e}}} = \dfrac{1}{{{v_e}}} - \dfrac{1}{{{f_e}}}$
$\Rightarrow \dfrac{1}{{{u_e}}} = \dfrac{1}{{25}} - \dfrac{1}{{2.5}}$
$\therefore {u_e} = - 2.27\,cm$
The image of the objective lens forms the object of the eyepiece. So, if we add the image distance of the objective lens and the object instance of the eyepiece, we will get the separation between the two lenses.
The separation can be calculated as
${\text{seperation}} = \left| {{v_o}} \right| + \left| {{u_e}} \right|$
$\therefore {\text{seperation}} = 7.2 + 2.27 = 9.47\,cm$
This is the distance between the two lenses.
The equation for finding the magnifying power of microscope is given as
$m = \dfrac{{{v_o}}}{{\left| {{u_o}} \right|}}\left( {1 + \dfrac{d}{{{f_e}}}} \right)$
Where, ${v_o}$ is the image distance of objective lens, ${u_o}$ is the object distance of objective lens, $d$ is the distance of near point and ${f_e}$ is the focal length of eyepiece.
On substituting the values in this equation, we get
$m = \dfrac{{7.2}}{{0.9}}\left( {1 + \dfrac{{25}}{{2.5}}} \right)$
$\therefore m = 88$
This is the value of magnifying power of the microscope.

Note: Remember that following the sign convention we took the object distance which is on the left side of the lens as negative and the image distance which is on the right side of lens as positive for both the lenses. Also remember that the image of the objective lens forms the object of the eye piece. That is why we get the separation as the sum of image distance of objective and the object distance of eye piece.