Question

A person wishes to distinguish between two pillars located at a distance of $11\,km$. What should be the minimum distance between these pillars?
A. $1\,m$
B. $3\,m$
C. $0.5\,m$
D. $5\,m$

Answer 1

The limits of resolution of the eyes, the conversion to radians, the formula for resolving power and more of such facts has to be known for this solution to be found. Resolving power is the ability of an instrument in distinguishing two very closely placed objects.

Formulas used:
$\theta = \dfrac{x}{d}$

Complete step by step answer:
The following are the given facts, the pillars are located at a distance of $11\,km$ from the person who wished to distinguish them. Let us recall the standard value of the resolving power of a human eye, $\theta = 1'$. Converting this to degrees, we arrive at the value,
$1' = {\left( {\dfrac{1}{{60}}} \right)^\circ }$
Converting the value in degrees to radians, we arrive at $\dfrac{\pi }{{60 \times 80}}$. Now considering the diagram given below, we have to find the value of the unknown $x$.

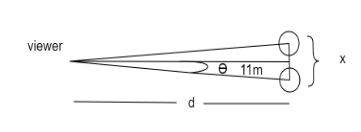
Our objective is to find the value of the unknown which is the distance between the two pillars. Now that we have the value of the angle made by the triangle using the vertices as the viewer and the two pillars, we can easily find the value of the unknown.The formula is,
$\theta = \dfrac{x}{d}$

\Rightarrow x = \dfrac{\pi }{{60 \times 180}} \times 11 \times {10^3}m \\\ \Rightarrow x = 3.2\,m$$ We have the answer as $$3.2m$$ but we make it a whole number by rounding off to the nearest integer. **Therefore, the correct answer is option B.** **Note:** The value of the distance between the viewer and the pillars is given in kilometers, this must be converted. The value of the resolving power of the human eye must be known and it should be converted into radians as we know that the formula given works only for theta in radians.