Question

- A person wears normal spectacles in which the distance of glasses and eyes is approximately 2cm, then power required is $- 5\,{\text{D}}$. If he wears contact lens, then the required power is
A. $- 5.2\,{\text{D}}$
B. $- 4.54\,{\text{D}}$
C. $+ 5.2\,{\text{D}}$
D. $+ 4.7\,{\text{D}}$

Answer 1

For normal spectacles, the object's distance can be infinite. Use lens formula to determine the focal length of the spectacle. Using the relation between power and focal length, determine the image distance. Again, use lens formula to determine the focal length of contact lens.

Formula used:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Here, f is the focal length of the lens, v is the image distance and u is the object distance.

Complete step by step solution:
We know that, for normal spectacles, the object's distance can be infinite. The normal spectacles are made up of concave lenses. Therefore, the image distance and object distance both are negative.
We assume the image position by using the spectacles is x cm from the lens.
We have the lens equation,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Here, f is the focal length of the lens, v is the image distance and u is the object distance.
Substituting x for v and $- \infty$ for u in the above equation, we get,
$\dfrac{1}{f} = \dfrac{1}{{ - x}} - \dfrac{1}{{ - \infty }}$
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{{ - x}}$
$\Rightarrow f = - x\,cm$
We have given the power of this spectacle is$- 5\,{\text{D}}$. We know the formula for power of the lens,
$P = \dfrac{1}{f}$
$\Rightarrow P = \dfrac{1}{f} = - 5\,{\text{D}}$
We substitute $- x\,cm$ for f in the above equation.
$\dfrac{1}{{ - x\,cm}} = - 5$
$\Rightarrow \dfrac{1}{{\left( { - x} \right) \times {{10}^{ - 2}}\,m}} = - 5$
$\Rightarrow \dfrac{{100}}{{ - x}} = - 5$
$\Rightarrow x = 20\,cm$
We know that for contact lenses, the image forms at infinity. Therefore, the image distance is infinite.

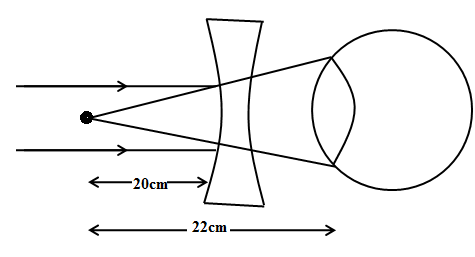
We can use lens equation to get the focal length of the contact lens as follows,
$\dfrac{1}{f} = \dfrac{1}{{ - \infty }} - \dfrac{1}{{22\,cm}}$
$\Rightarrow \dfrac{1}{f} = - \dfrac{1}{{22\,cm}}$
$\Rightarrow f = - 22\,cm$
Now, the power of this contact lens is,
$P = \dfrac{1}{f}$
Substitute $- 22\,cm$ for f in the above equation.
$P = \dfrac{{100}}{{ - 22}}$
$\Rightarrow P = - 4.54\,D$
Therefore, the power of the contact lens will be $- 4.54\,D$.

So, the correct answer is “Option B”.

Note:
The factor 100 in the formula for power is due to the fact that the power is always expressed in units of per meter.
Since our given values are in cm, we have taken the factor 100 to multiply it.
Remember, the power of a concave lens is always negative.