Question
Question: A person walks along an east-west street and a graph of his displacement from home is shown in the f...
A person walks along an east-west street and a graph of his displacement from home is shown in the figure. His average velocity for the whole time interval is.
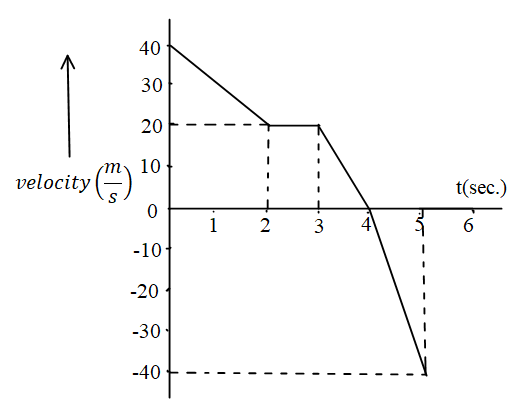
A) 0sm
B) 23sm
C) 8.4sm
D) None of the above
Solution
The area of the velocity and time graph will give the distance travelled by the body so in order to get the distance travelled by the person we can just take out the area of the velocity-time graph.
Complete step by step answer:
The person walks with some velocity and the variation of distance with respect to time is been recorded and given in the form of a graph also we know now that the area of velocity-time graph will give distance travelled by the person. So let us calculate the distance travelled by the person.
The area of the velocity-time graph will give the distance travelled by the person.
Area of the graph is equal to,
Total area= (Ar. of trapezium from t=0s to t=2s) + (Ar. of rectangle from t=2s to t=3s) + (Ar. of triangle from t=3s to t=4s)-(Ar. of triangle from t=4s to t=5s).
Let us calculate the area of different time interval respectively.
Area of graph for the time interval of time t=0s to t=2s.
⇒Ar. of trapezium from (t=0s to t=2s)=21⋅(40+20)⋅(2)
⇒Ar. of trapezium from (t=0s to t=2s)=21⋅(60)⋅(2)
⇒Ar. of trapezium from (t=0s to t=2s)=60m………eq. (1)
Area of the rectangle from t=2s to t=3s.
⇒Ar. of rectangle from (t=2s to t=3s)=20×(3−2)
⇒Ar. of rectangle from (t=2s to t=3s)=20×1
⇒Ar. of rectangle from (t=2s to t=3s)=20m………eq. (2)
Area of the triangle from t=3s to t=4s.
⇒Ar. of triangle from (t=3s to t=4s)=21×20×(4−3)
⇒Ar. of triangle from (t=3s to t=4s)=21×20×1
⇒Ar. of triangle from (t=3s to t=4s)=10m………eq. (3)
Area of the triangle from t=4s to t=5s.
⇒Ar. of triangle from (t=4s to t=5s)=21×(5−4)×(−40)
⇒Ar. of triangle from (t=4s to t=5s)=21×(−40)
⇒Ar. of triangle from (t=4s to t=5s)=−20m………eq. (4)
Since,
Total area= (Ar. of trapezium from t=0s to t=2s) + (Ar. of rectangle from t=2s to t=3s) + (Ar. of triangle from t=3s to t=4s)-(Ar. of triangle from t=4s to t=5s).
Therefore,
⇒Total area=60m+20m+10m−20m
⇒Total area=60m+10m
⇒Total area=70m
As the total distance travelled by the person in the area of the velocity-time graph of the person.
⇒s=70m
Therefore, the total distance travelled by the person is equal to s=70m.
As the average is defined as the ratio of total distance upon the total time taken.
⇒Vavg=ts
⇒Vavg=570
⇒Vavg=14ms−1.
Therefore, the correct option for this problem is option (D).
Note:
The area of the graph velocity-time graph is equal to the distance travelled this concept should be well known by the students there are few more relations which tells us about some physical quantity. It should be observed that the sign of the area of the graph below the x-axis is taken as negative as the person is walking backwards.
