Question

A person walking along a straight road observes that at two points 1 km apart, the angles of elevation of a pole in front of him are ${{30}^{{}^\circ }}$ and ${{75}^{{}^\circ }}$. The height of the pole is
A.$500\left( \sqrt{3}+3 \right)m$
B.$250\left( \sqrt{3}+1 \right)m$
C.$250\left( \sqrt{2}+1 \right)m$
D.$250\left( \sqrt{2}-1 \right)m$

Answer 1

Hint:Draw a diagram with given information and then use the formula $\tan \theta =\dfrac{opposite\text{ }side}{hypotenuse}$ for both the given angles; you will get two simultaneous equations. Use the results $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$ and $\tan 75{}^\circ =\left( \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \right)$ in the equations and solve them to get the final answer.

Complete step by step answer:
To solve the above problem we will construct a diagram with given conditions and then we will write the given data accordingly,
,
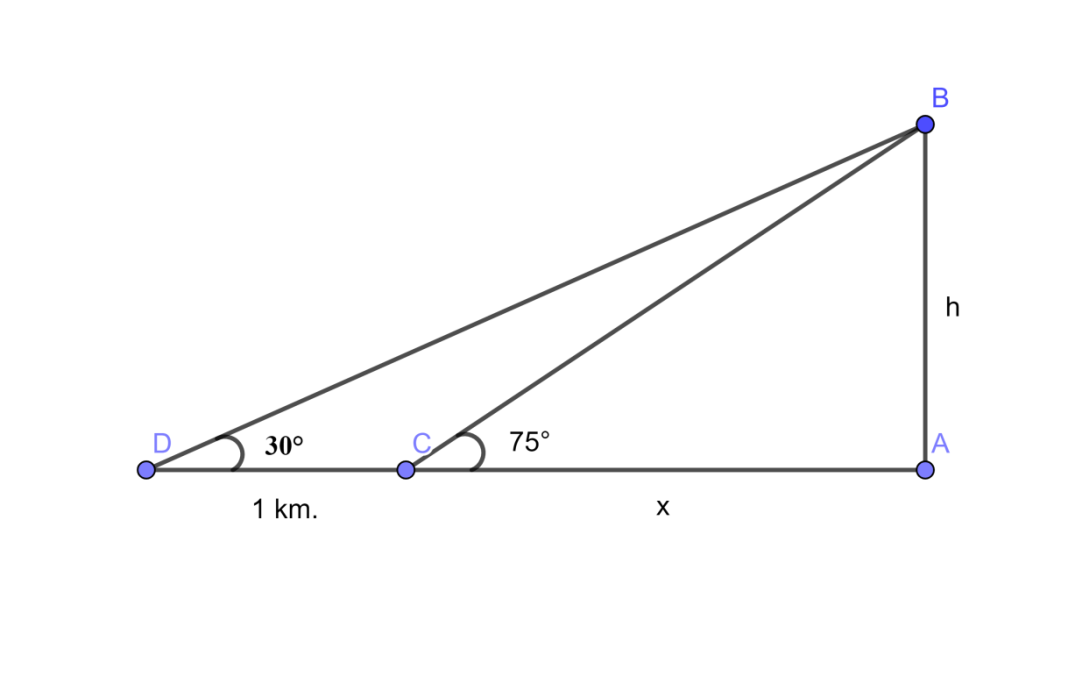
Now, we have constructed the diagram with given conditions therefore now we will write the given data with assuming the notations given in the diagram for it.
Distance between two points = DC = 1 km. ………………………………………….. (1)
$\angle D=30{}^\circ$ and $\angle C=75{}^\circ$ ……………………………………………………………….. (2)
Also assume,
The distance between point C and point A = CA = x ………………………………………… (3)
Height of the pole = BA = h ……………………………………………………………………………. (4)
As we have to find the height of the pole and we have given the value of difference between the two points D and C therefore we should use the trigonometric function which will take this tow values in consideration.
As we know that the function ‘tan’ considers the opposite side which is height in this case and the hypotenuse which considers the difference of two points in this case therefore we will use the ‘tan’ function to find the height of the pole.
Therefore,
As we know, $\tan \theta =\dfrac{opposite\text{ }side}{hypotenuse}$ therefore by using this formula we can write,
$\tan D=\dfrac{BA}{DA}$
From diagram we can replace DA by DC + CA and therefore above equation will become,
$\tan D=\dfrac{BA}{DC+CA}$
If we put the values of equation (1), equation (2), equation (3) and equation (4) in the above equation we will get,
$\tan 30{}^\circ =\dfrac{h}{1+x}$ ………………………………………………………. (4)
Also,
$\tan C=\dfrac{BA}{CA}$
If we put the values of equation (2), equation (3) and equation (4) in the above equation we will get,
$\therefore \tan 75{}^\circ =\dfrac{h}{x}$
$\therefore h=x\tan 75{}^\circ$ ………………………………………………………………………. (6)
If we put the value of equation (6) in the equation (5) we will get,
$\therefore \tan 30{}^\circ =\dfrac{x\tan 75{}^\circ }{1+x}$
As we know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$ and $\tan 75{}^\circ =\left( \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \right)$ and if we put this values in the above equation we will get,
$\therefore \left( 1+x \right)\dfrac{1}{\sqrt{3}}=x\left( \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \right)$
$\therefore \left( 1+x \right)\left( \sqrt{3}-1 \right)=\sqrt{3}\times x\left( \sqrt{3}+1 \right)$
$\therefore \sqrt{3}\left( 1+x \right)-\left( 1+x \right)=\sqrt{3}x\times \sqrt{3}+\sqrt{3}x$
$\therefore \sqrt{3}+\sqrt{3}x-1-x=3x+\sqrt{3}x$
$\therefore \sqrt{3}-1-x=3x$
$\therefore \sqrt{3}-1=3x+x$
$\therefore \sqrt{3}-1=4x$
$\therefore x=\dfrac{\sqrt{3}-1}{4}km.$
If we put the above value in equation (6) we will get,
$\therefore h=\dfrac{\sqrt{3}-1}{4}\times \tan 75{}^\circ$
Also if we put $\tan 75{}^\circ =\left( \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \right)$ in the above equation we will get,
$\therefore h=\dfrac{\sqrt{3}-1}{4}\times \left( \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \right)$
$\therefore h=\dfrac{\sqrt{3}+1}{4}km$
As we have our solution in terms of meters therefore we will convert our solution in meters by simply multiplying it by 1000, therefore we will get,
$\therefore h=\left( \dfrac{\sqrt{3}+1}{4}\times 1000 \right)m$
$\therefore h=250\left( \sqrt{3}+1 \right)m$
Therefore the height of the pole is equal to $250\left( \sqrt{3}+1 \right)m$.
Therefore the correct answer is option (b).

Note: If you don’t know the value of $\tan 75{}^\circ$ then convert it as $\tan \left( 45{}^\circ +30{}^\circ \right)$ and use the formula $\tan \left( A+B \right)=\dfrac{\tan A+\tan B}{1-\tan A\times \tan B}$, you will get the value.