Question

A person travelling eastwards at the rate of 2 m/s finds that the wind seems to blow directly from the north. On doubling its speed, it appears to come from the north east. Find the magnitude and direction of the wind.

Answer 1

As we need to find both vector and magnitude, we can use the concept of vectors (have both magnitude and direction). We can find the velocity of man, wind and both with respect to each other in vector form in both the cases and find the required magnitude and direction of the wind.
The vector A with respect to B is given as:
${V_{AB}} = {V_A} - {V_B}$

Complete step by step answer:
The person is travelling towards the east i.e. positive direction of x – axis at the rate of 2 m/s. So, it velocity in vector form is given as:
${V_M} = 2\hat i$

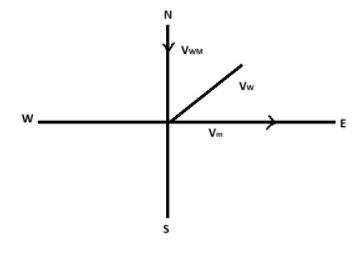
As the wind in general would be along both the axis, let its velocity in vector form be:
${V_W} = a\hat i + b\hat j$ ________ (A)
It is given that for the man, the wind seems to blow directly from the north i.e. velocity of wind with respect to the man is only along the y – axis:
${V_{WM}} = 0\hat i + b\hat j \\\ \implies {V_{WM}} = b\hat j \\\$
Now, the velocity of wind with respect to the man mathematically is given as:
${V_{WM}} = {V_W} - {V_M}$
Substituting the values, we get:
$0\hat i + b\hat j = a\hat i + b\hat j - 2\hat i$
Equating L.H.S and R.H.S for similar quantities:
$0\hat i = \left( {a - 2} \right)\hat i \\\ \Rightarrow \left( {a - 2} \right) = 0 \\\ \Rightarrow a = 2.....(1) \\\$
Now, when the speed of man is doubled,
Its velocity vector becomes:
${V_M} = 4\hat i\left( {\because 2 \times 2\hat i = 4\hat i} \right)$
The wind appears to come from the north east, thus it will be directed towards south east direction (from the origin), then velocity of wind with respect to the man is given as:
${V_{WM}} = a\hat i + b\hat j - 4\hat i \\\ \implies {V_{WM}} = (a - 4)\hat i + b\hat j \\\$

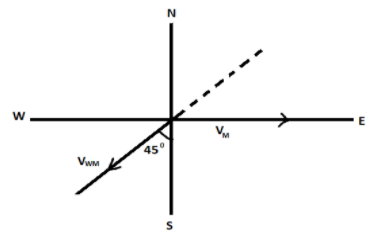
The angle formed is of 45° as the angle of 90° is bisected. Finding the value of tan for this angle:
$\tan \theta = \dfrac{P}{B}$ here,
$\implies \theta = {45^\circ }$
Perpendicular (P) is along the y – axis = b
Base (B) is along the x – axis = a – 4
$\tan 45 = \dfrac{b}{{a - 4}} \\\ \implies 1 = \dfrac{b}{{a - 4}}\left( {\because \tan 45 = 1} \right) \\\ \implies b = a - 4 \\\$
Substituting the value of a from (1):
$b = 2 - 4 \\\ \implies b = - 2 \\\$
Substituting the values of a and b in equation (A), we get:
${V_W} = 2\hat i - 2\hat j$
The magnitude of this vector is:
$\left| {{V_W}} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( { - 2} \right)}^2}} \\\ \implies \left| {{V_W}} \right| = 2.82 \\\$
Therefore, the magnitude of the velocity of the wind is 2.8 m/s (since given velocity is in m/s only) and its direction is south east.

Note:
$\hat i$ and $\hat j$ used here are known as unit vectors and are used to represent the vectors along x and y – axis respectively.
We use $\left| {} \right|$ brackets to denote the magnitude of any quantity. In the case of vectors, it is equal to the square root of the sum of the squares of quantities along respective axes. E.g. for a vector $x\hat i + y\hat j$, the magnitude will be given as $\sqrt {{x^2} + {y^2}}$