Question

A person swims in a river aiming to reach exactly on the opposite point on the bank of the river. His speed of swimming is 0.5 m/s at an angle $120^\circ$ with the direction of flow of water. The speed of water is
A. 1.0 m/s
B. 0.5 m/s
C. 0.25 m/s
D. 0.43 m/s

Answer 1

The given angle is the angle between the direction of the swimmer and downstream flow of water. Find the angle between the direction of the swimmer and perpendicular to the flow. Use the simple geometric construction to express the angle between velocity of man and velocity of man with respect to the river.

Complete step by step answer:
We assume the river is flowing in the rightward direction of the person. If the person swims perpendicular to the flow of water to reach the exact opposite of the bank, he will drift towards right due to the flow of water. So, for the person to reach exactly opposite of the bank, he should swim at an angle $120^\circ - 90^\circ = 30^\circ$ as shown in the following figure.

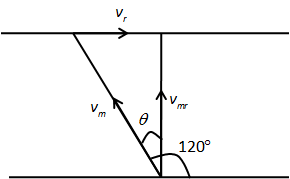
In the above figure, ${v_m}$ is the velocity of the man, ${v_{mr}}$ is the velocity of the man with respect to river, and ${v_r}$ is the velocity of river.

From the geometry of the above figure, we have,
$\sin \theta = \dfrac{{{v_r}}}{{{v_m}}}$
$\Rightarrow {v_r} = {v_m}\sin \theta$

Substitute $0.5\,m/s$ for ${v_m}$ and $30^\circ$ for $\theta$ in the above equation.
${v_r} = \left( {0.5} \right)\sin \left( {30^\circ } \right)$
$\Rightarrow {v_r} = 0.25\,m/s$

Therefore, the velocity of flow of the river is 0.25 m/s.

Note: Another way to solve this question is to calculate the horizontal component of the velocity of the person in the opposite direction of the flow. That is ${v_x} = \left( {0.5} \right)\cos \left( {180^\circ - 120^\circ } \right) = 0.25\,m/s$. Since the person is opposing the drift of flow and does not have horizontal motion, therefore, the downstream velocity is equal to the upstream velocity of flow.