Question

A person starts at the bottom left corner O(0, 0) of a rectangular grid and moves to the top right corner T(5, 4) by taking only one unit right or one unit up. All shortest path form O to T are equally likely. Then the probability that the path passes through P(2, 1) given that it will also pass through Q(4, 3) is

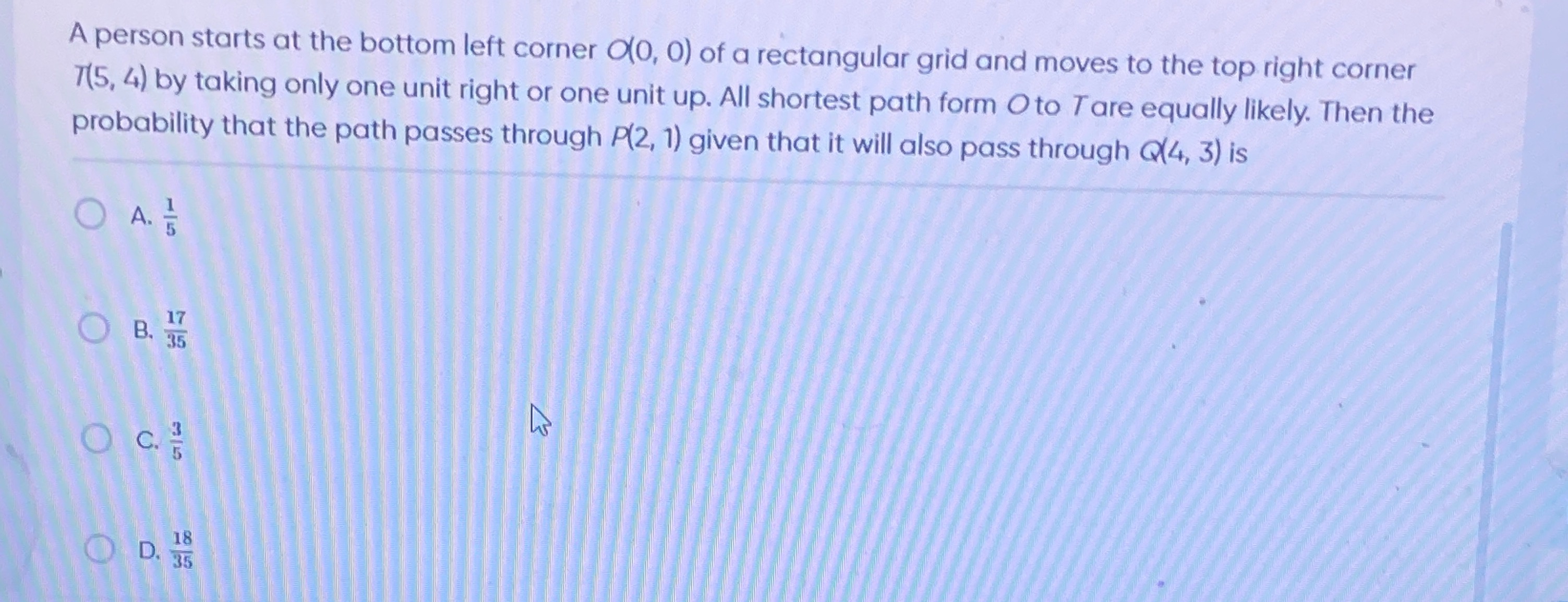
• A. $\frac{1}{5}$
• B. $\frac{17}{35}$
• C. $\frac{3}{5}$
• D. $\frac{18}{35}$

Answer 1

Answer: (D)

$\frac{18}{35}$

Answer 2

The number of shortest paths from $(x_1, y_1)$ to $(x_2, y_2)$ is $\binom{(x_2-x_1)+(y_2-y_1)}{x_2-x_1}$. The number of paths through Q(4,3) is $N(O \to Q) \times N(Q \to T) = \binom{4+3}{4} \times \binom{(5-4)+(4-3)}{5-4} = \binom{7}{4} \times \binom{2}{1} = 35 \times 2 = 70$. The number of paths through P(2,1) and Q(4,3) is $N(O \to P) \times N(P \to Q) \times N(Q \to T) = \binom{2+1}{2} \times \binom{(4-2)+(3-1)}{4-2} \times \binom{(5-4)+(4-3)}{5-4} = \binom{3}{2} \times \binom{4}{2} \times \binom{2}{1} = 3 \times 6 \times 2 = 36$. The conditional probability is the ratio of these counts: $\frac{36}{70} = \frac{18}{35}$.