Question

A person stands in contact against the inner wall of the rotor of radius r. The coefficient of friction between the wall and the clothing is $\mu$ and the rotor is rotating about the vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
A. $\sqrt{\dfrac{\mu g}{r}}$
B. $\sqrt{\dfrac{\mu r}{g}}$
C. $\sqrt{\dfrac{ g}{\mu r}}$
D. $\sqrt{\mu r g}$

Answer 1

The motion of the man is a circular motion. The problem is about balancing the force of gravity out so that the man performs a circular motion and does not fall. There are two forces that are helping in achieving this, one is the inwards centripetal force and another is frictional force.

Complete answer:
Let's take a note if the forces involved first:

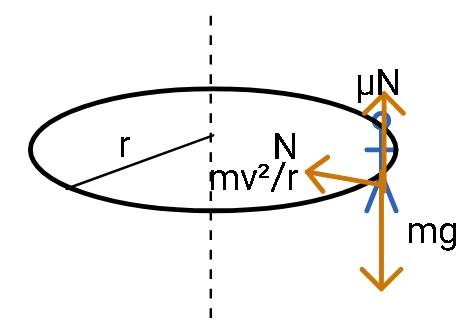
1. Weight of the person (mg) acts in a downward direction.
2. A normal force acts perpendicular to the surface (towards the center).
3. A centripetal force acts (due to circular motion) towards the centre with magnitude $m \omega^2 r$ where m is the mass, $\omega$ is angular velocity and r is the distance from the axis.
4. A frictional force acts opposite in direction to the downward force (mg).

Now, we can conclude that the normal force is equal to the centripetal force. Therefore,
$N = m \omega^2 r$.
We know that a frictional force is given the expression:
$f= \mu N$
Keeping the value of N, we get

$f = \mu m \omega^2 r$.
This frictional force is balancing the download force i.e., the weight of the body. Upon equating the two forces, we get:
$mg = \mu m \omega^2 r$.
Cancelling the m on both sides:
$g = \mu \omega^2 r$.
We are asked to find the minimum angular velocity $\omega$,
So,
$\omega = \sqrt{\dfrac{g}{\mu r}}$

So, the correct answer is “Option C”.

Note:
The condition for minimum velocity is when the friction completely balances mg; beyond this minimum angular velocity, the person certainly continues the circular motion and has no chance of falling down. If the angular velocity is lower than the minimum value, gravity dominates and the person falls.