Question
Question: A person standing at a distance of 6m from a source receives sound waves in two ways, one directly f...
A person standing at a distance of 6m from a source receives sound waves in two ways, one directly from the source and other after reflection from a rigid boundary as shown in the figure. The maximum wavelength for which, the person will receive maximum sound intensity is:
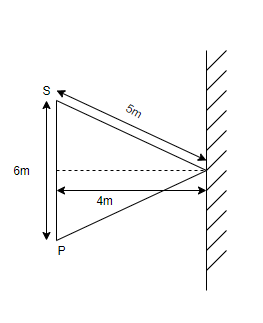
A.4m B.316m C.2m D.38m
Solution
- Hint – Here we will proceed by using the formula for wavelength. It is inversely related to frequency, which refers to the number of wave cycles per second. The higher the frequency of the signal, the shorter the wavelength.
Formula used : λ=fv
Where wavelength is denoted by λ
V= velocity of the wave
F= frequency.
Complete step-by-step solution -
Here it is given that distance between the person and the source receives sound waves =6m.
And it is also given that the sound waves received from a source in two ways. One is directly from the source and the other is after reflection from a rigid boundary.
We have to find out the maximum wavelength for which, the person will receive maximum sound intensity
For the intensity to be maximum after interference, the path difference between the two waves must be an integral multiple of wavelength.
Therefore, (5+5)−6=nλ (∵ intensity is given by nλ)
⇒(10−6)=nλ
⇒4=nλ ⇒λ=n4
The value of wavelength (λ) is maximum for a minimum value of n, which is 1.
Therefore, the maximum value of λ will be,
λmax=14
⇒λmax=4m
Note – Whenever we come up with this type of question, where we are asked to find out the maximum wavelength. Then we first write the formula and then in place of the formula we put the values of the quantity. After solving that we will get the maximum sound intensity. In this way we will get our answer.
