Question

A person on the top of a tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from ${30^ \circ }$ to ${45^ \circ }$ how soon after this, will the car reach the tower?

Answer 1

Complete step by step answer:

Let us first draw the diagram of the given condition.

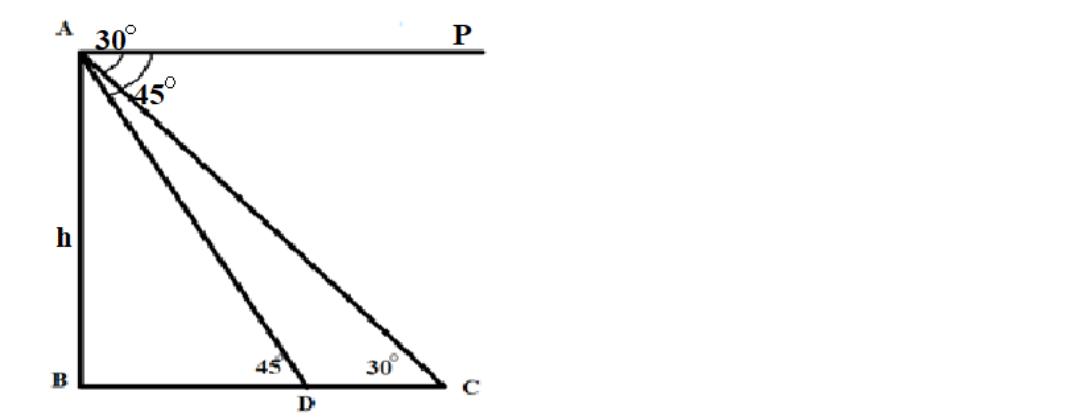
Let A be the point where the man is standing on the tower. Let AB be the height of the tower, denoted by $h$. Now, the car is moving such that ${30^ \circ }$ to ${45^ \circ }$.
We will first find the distance of $BD$.
Also, we know that distance is the product of speed and time.
The distance covered is $BD$ from the foot of the tower which is equal to the product of velocity and time.
That is , ${\text{BD}} = vt$, where $v$ is the speed of the car and $t$ is the time.
We will use this relation to calculate the height $h$
Now, consider $\vartriangle {\text{ABC}}$ and find the value of $\tan {45^ \circ }$
We know that $\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$
Then, $\tan {45^ \circ } = \dfrac{{AB}}{{BD}}$
Also, $\tan {45^ \circ } = 1$ and ${\text{AB}} = h$
Then,
$1 = \dfrac{h}{{vt}} \\\ \Rightarrow h = vt \\\$
Now, consider the $\vartriangle ABD$
Then, $\tan {30^ \circ } = \dfrac{{AB}}{{BD}}$
$\tan {30^ \circ } = \dfrac{{AB}}{{BC + CD}}$
Here, $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
We are given that the time taken to reach from angle ${30^ \circ }$ to ${45^ \circ }$ is 12 minutes.
If $v$ is the speed of the car, then the distance covered is $12v$
On substituting the values, we get,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{12v + vt}}$
We have already proved that $h = vt$
Hence, the expression cam now be written as $\dfrac{1}{{\sqrt 3 }} = \dfrac{{vt}}{{12v + vt}}$
Cross-multiply the expression and solve for the value of $t$
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{vt}}{{12v + vt}} \\\ \Rightarrow 12v + vt = \sqrt 3 vt \\\ \Rightarrow \left( {\sqrt 3 - 1} \right)vt = 12v \\\ \Rightarrow t = \dfrac{{12}}{{\sqrt 3 - 1}} \\\$
Now, $\sqrt 3 = 1.73$
Therefore,
$t = \dfrac{{12}}{{1.73 - 1}} \\\ \Rightarrow t = \dfrac{{12}}{{0.73}} \\\ \Rightarrow t = \dfrac{{1200}}{{73}} \\\ \Rightarrow t = 16.43 \\\$
Hence, the car will take 16.43 minutes after point D to reach the tower.

Note: If the angle is formed from the person looking up at some object, then the angle formed from horizontal to the object is known as angle of elevation. Here, ${30^ \circ }$ and ${45^ \circ }$ are angles of elevation. In this question concept of speed, time, and distance are also used besides concepts of trigonometry.