Question

A person on the top of a tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from $30^\circ$ to $45^\circ$ how soon after this, will the car reach the tower?

Answer 1

First we will assume that the height of the tower is AD. Then we will take the right angle triangle $\Delta {\text{ACD}}$ and use the tangential property, that is, $\tan C = \dfrac{p}{b}$, where $p$ is the perpendicular and $b$ is the base and then use the same property in the right angle triangle $\Delta {\text{ABD}}$. Then we use the given to find the required value.

Complete step by step answer:

Let us assume that the height of the tower is AD.

We are given that man sees car first at an angle of depression of $30^\circ$, so $\angle PAB = 30^\circ$, after 12 minutes, the man sees car at an angle of depression of $45^\circ$, so $PAC = 45^\circ$ and BC is 12.

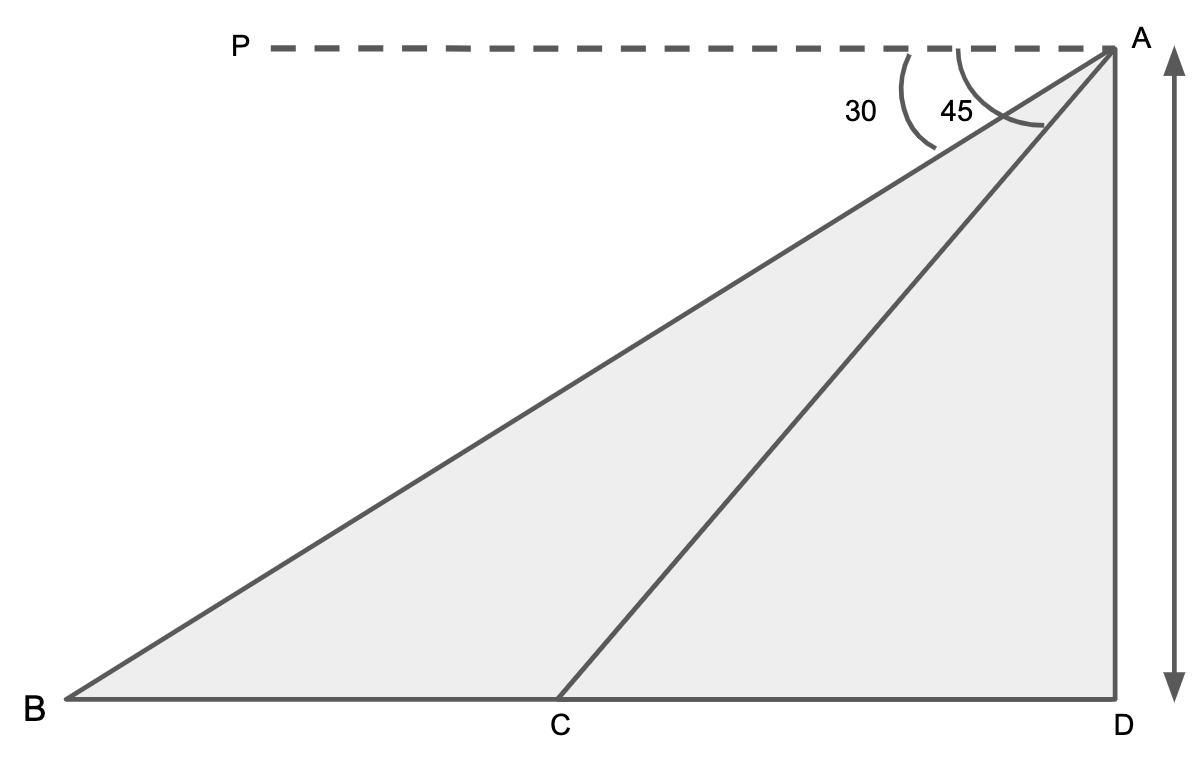
Now we know that the tower is vertical, so $\angle ADB = 90^\circ$.

Also, since the angle of elevation is equal to the angle of depression, so we have

$$\Rightarrow \angle ABD = \angle PAB \\\ \Rightarrow \angle ABD = 30^\circ \\\$$ $$\Rightarrow \angle ACD = \angle PAC \\\ \Rightarrow \angle ACD = 45^\circ \\\$$

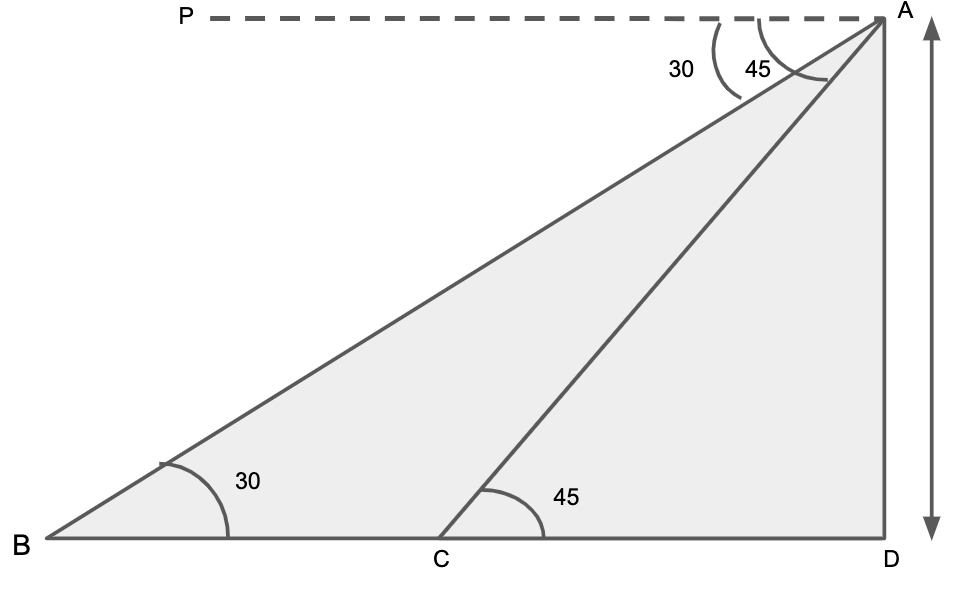
Let us also assume that $CD$ is $\alpha$ .

First, we will take the right angle triangle $\Delta {\text{ACD}}$.
We will use the tangential property, that is, $\tan C = \dfrac{p}{b}$, where $p$ is the perpendicular and $b$ is the base.

Using the above tangential property, we get

$\tan C = \dfrac{{{\text{AD}}}}{{{\text{CD}}}}$

Substituting the value of angle C in the above equation, we get

$$\Rightarrow \tan 45^\circ = \dfrac{{AD}}{{CD}} \\\ \Rightarrow 1 = \dfrac{{AD}}{{CD}} \\\$$

Multiplying the above equation by CD on both sides, we get

$$\Rightarrow CD = AD \\\ \Rightarrow AD = CD{\text{ ......eq.(1)}} \\\$$

We will now take the right angle triangle $\Delta {\text{ABD}}$,

We will use the tangential property, that is, $\tan {\text{B}} = \dfrac{p}{b}$, where $p$ is the perpendicular and $b$ is the base.

Using the above tangential property, we get

$\tan B = \dfrac{{{\text{AD}}}}{{{\text{BD}}}}$

Substituting the value of angle B in the above equation, we get

$$\Rightarrow \tan 30^\circ = \dfrac{{AD}}{{BD}} \\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{AD}}{{BD}} \\\$$

Cross-multiplying the above equation, we get

$$\Rightarrow \dfrac{{BD}}{{\sqrt 3 }} = AD \\\ \Rightarrow AD = \dfrac{{BD}}{{\sqrt 3 }}{\text{ ......eq.(2)}} \\\$$

From equation (1) and equation (2), we get
$\Rightarrow CD = \dfrac{{BD}}{{\sqrt 3 }}$

Multiplying the above equation by $\sqrt 3$ on both sides, we get
$\Rightarrow \sqrt 3 CD = BD$

Using the sum of $BC$ and $CD$ for BD from the given figure in the above equation, we get
$\Rightarrow \sqrt 3 CD = BC + CD$

Subtracting the above equation by CD on both sides, we get

$$\Rightarrow \sqrt 3 CD - CD = BC + CD - CD \\\ \Rightarrow \left( {\sqrt 3 - 1} \right)CD = BC \\\$$

Dividing the above equation by $\sqrt 3 - 1$ on both sides, we get

$$\Rightarrow \dfrac{{\left( {\sqrt 3 - 1} \right)CD}}{{\sqrt 3 - 1}} = \dfrac{{BC}}{{\sqrt 3 - 1}} \\\ \Rightarrow CD = \dfrac{{BC}}{{\sqrt 3 - 1}} \\\$$

Rationalizing the above equation by multiplying denominator and numerator with $\sqrt 3 + 1$, we get

$$\Rightarrow CD = \dfrac{{BC}}{{\sqrt 3 - 1}} \times \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}} \\\ \Rightarrow CD = \dfrac{{BC\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}} \\\$$

Using the above property ${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$ in the above equation, we get

$$\Rightarrow CD = \dfrac{{BC\left( {\sqrt 3 + 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - {1^2}}} \\\ \Rightarrow CD = \dfrac{{BC\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} \\\ \Rightarrow CD = \dfrac{{BC\left( {\sqrt 3 + 1} \right)}}{2} \\\$$

Substituting the value of BC in the above equation to find the time taken to cover CD, we get

$$\Rightarrow CD = \dfrac{{12\left( {\sqrt 3 + 1} \right)}}{2} \\\ \Rightarrow CD = 6\left( {\sqrt 3 + 1} \right){\text{ minutes}} \\\$$

Hence, it takes $6\left( {\sqrt 3 + 1} \right)$ minutes to reach to the foot of the tower.

Note: In solving these types of questions, you should be familiar with the concept of angle of depression and the tangential properties. Students should make the diagram for better understanding. Using the values of respective angles you can simply find any length present in the figure using the tangential value ‘$\tan$’, which makes our problem easy to solve. Students need to write the units in the final answer or else the answer will be partially wrong.