Question

A person of mass $m$ is standing at one edge of a boat of length $l$ ; if he walks a distance $x$ towards the shore, then what is the distance moved by the boat in the backward direction?

Answer 1

Hint To solve this question, we have to find out the change in the position of the centre of mass of the system. Then applying Newton's second law of motion, we can easily get the answer.
Center of Mass of a system of 2 bodies is given as,
$\Rightarrow {x_{COM}} = \dfrac{{{x_1}{m_1} + {x_2}{m_2}}}{{{m_1} + {m_2}}}$
Here, ${x_{COM}}$ is position of center of mass, ${x_1}$ is position of 1st body, ${x_2}$ is position of 2nd body, ${m_1}$ is mass of 1st body, and ${m_2}$ is mass of 2nd body

Complete step by step answer
Here we should understand that the boat and the man together make a system. So, this system will have a center of mass. Thus the change in center of mass of the system will then give us the distance moved by the boat.
Since while finding the center of mass of a system, we can choose our own reference coordinate system, so, the most appropriate coordinate system will be the one that requires the easy and less calculations. So, let us take the origin of the system to be that edge of the boat where the man is standing.

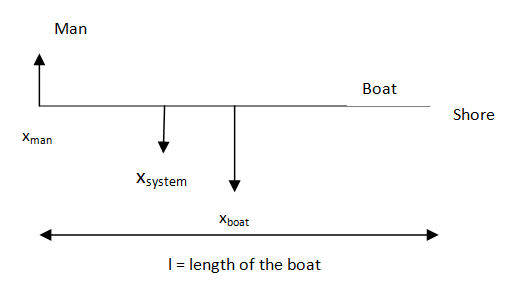
Let the mass of the boat be $M$ . It is given that the mass of the man is $m$ . Now, with the reference frame we chose, we get the center of mass of the boat ${x_{boat}} = \dfrac{l}{2}$ and center of mass of the man ${x_{man}} = 0$ . This gives the position of the center of mass of the system as
$\Rightarrow {x_{system}} = \dfrac{{{x_{man}}m + {x_{boat}}M}}{{m + M}}$
Now, putting in the values we get
$\Rightarrow {x_{system}} = \dfrac{{(0)(m) + (\dfrac{l}{2})M}}{{m + M}} \\\ \Rightarrow {x_{system}} = \dfrac{{Ml}}{{2(m + M)}} \\\$

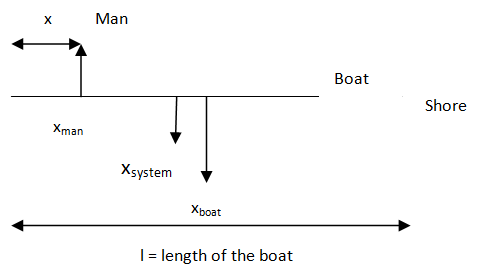
This is the initial position of the center of mass of the system. When the man moves $x$ distance forward towards the shore, by Newton’s third law the boat would move backwards. Thus there will be a shift in center of mass of the system.
This time the position of man would not be zero but $x$ as the man moved $x$ units to the right of the origin. So, we would get,
$\Rightarrow {x_{system}} = \dfrac{{(x)(m) + (\dfrac{l}{2})M}}{{m + M}} \\\ \Rightarrow {x_{system}} = \dfrac{{Ml + 2x_m}}{{2(m + M)}} \\\$
Thus, the change in the position of the center of mass of the system would be,
$\Rightarrow {x_{system}} = \dfrac{{2x_m + Ml}}{{2(m + M)}} - \dfrac{{Ml}}{{2(m + M)}}$
$\Rightarrow {x_{system}} = \dfrac{{2x_m}}{{2(m + M)}}$
This gives the change in the position of the center of mass of the system as,
$\Rightarrow {x_{system}} = \dfrac{{x_m}}{{(m + M)}}$
Now, if the boat moves $d$ distance backwards, then,
$\Rightarrow {x_{system}}{m_{system}} = d{m_{boat}}$
$\Rightarrow \dfrac{{x_m}}{{(m + M)}}(m + M) = dM$
$(m + M)$ gets cancelled and we get,
$\Rightarrow x_m = dM$
$\Rightarrow d = \dfrac{{x_m}}{M}$
$\therefore$ The boat moved backwards by a distance of $\dfrac{{x_m}}{M}$ units.

Note
Always remember that the Newton’s third Law talks about equal and opposite ‘Forces’. It does not tell us about any other quantity such as velocity or distance. Thus, the force acting on the man and the boat due to each other would be equal and opposite, but the distance moved by them can be different.