Question

A person observed the angle of elevation of a tower as ${{30}^{\circ }}$. He walked from 50 m towards the fort of the tower along level ground and found the angle of elevation of the top of the tower as ${{60}^{\circ }}$. Find the length of the tower.

Answer 1

Hint:First of all we will suppose the tower to be AB where A is the top and B is the bottom of the tower. Now we will complete the diagram by considering point C as a starting point where a person is observing the tower with angle of elevation made with respect to ground and after covering some distance consider it as point D where another angle of elevation is made with respect to ground and the distance between two points AD is given.Then we will use the trigonometric ratio to find the height of the tower. Also, we know that angle of elevation means the angle from horizontal upward to an object.

Complete step-by-step answer:
We have been given the angle of elevation of tower is ${{30}^{\circ }}$ as observed by a man and after a 50 m distance towards the foot of the tower along level ground the angle of elevation of the top of tower is ${{60}^{\circ }}$.
Let us assume the tower to be AB and C be the point where the angle of elevation is ${{30}^{\circ }}$ and D be the point where angle of elevation is ${{60}^{\circ }}$and the distance between C and D points is equal to 50 m.

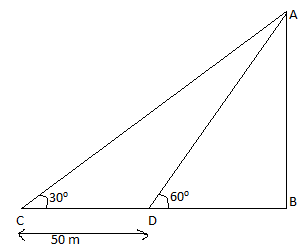
Let us consider $\Delta ABC$,
$\tan C=\dfrac{AB}{BC}$
Since $\angle C={{30}^{\circ }}$ and $BC=BD+CD=\left( BD+50 \right)m$
$\Rightarrow \tan {{30}^{\circ }}=\dfrac{AB}{\left( BD+50 \right)}$
We know that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$.
Substituting in above equation,we get
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{AB}{BD+50}$
On cross multiplication, we get as follows:

& BD+50=AB\sqrt{3} \\\ & \Rightarrow BD+AB\sqrt{3}-50......(1) \\\ \end{aligned}$$ Again in $$\Delta ABD$$, $$\tan D=\dfrac{AB}{BD}$$ Since $$\angle D={{60}^{\circ }}$$ and $$BD=AB\sqrt{3}-50$$ from equation (1). $$\Rightarrow \tan {{60}^{\circ }}=\dfrac{AB}{AB\sqrt{3}-50}$$ We know that $$\tan {{60}^{\circ }}=\sqrt{3}$$. $$\Rightarrow \sqrt{3}=\dfrac{AB}{AB\sqrt{3}-50}$$ On cross multiplication, we get as follows: $$\begin{aligned} & \Rightarrow AB\sqrt{3}\times \sqrt{3}-50\sqrt{3}=AB \\\ & \Rightarrow AB{{\left( \sqrt{3} \right)}^{2}}-50\sqrt{3}=AB \\\ & \Rightarrow 3AB-50\sqrt{3}=AB \\\ \end{aligned}$$ On taking AB to the left hand side, we get as follows: $$\begin{aligned} & 3AB-AB-50\sqrt{3}=0 \\\ & \Rightarrow 2AB-50\sqrt{3}=0 \\\ \end{aligned}$$ On taking $$50\sqrt{3}$$ to the right hand side, we get as follows: $$2AB=50\sqrt{3}$$ On dividing by 2 we get as follows: $$\begin{aligned} & \dfrac{2AB}{2}=\dfrac{50\sqrt{3}}{2} \\\ & \Rightarrow AB=25\sqrt{3}m \\\ \end{aligned}$$ We also know that $$\sqrt{3}=1.732$$ (approximately). $$\begin{aligned} & \Rightarrow AB=25\times 1.732 \\\ & \Rightarrow AB=43.300m \\\ \end{aligned}$$ Therefore, the required height of the tower is equal to 43.3m. Note: In this type of question, you must have to draw the diagram according to the condition given in the question and then move further for calculation. Also, be careful while drawing the diagram and mark the angles 30 degrees and 60 degrees correctly according to the question otherwise we will get incorrect answers. Also, don’t get confused about the value of $$\tan {{60}^{\circ }}$$. Sometimes we use $$\tan {{60}^{\circ }}=\dfrac{1}{\sqrt{3}}$$ and $$\tan {{30}^{\circ }}=\sqrt{3}$$ which is wrong. So take care of it while calculating.Students should remember the important trigonometric ratios and standard angles to solve these types of questions.