Question

A person normally weighing $60kg$ stands on a platform which oscillates up and down simple harmonically with a frequency $2Hz$ and an amplitude $5cm$ . If a machine on the platform gives the person’s weight then consider the following statements.
A. The maximum reading of the machine will be $108kg$ .
B. The maximum reading of the machine will be $90kg$ .
C. The minimum reading of the machine will be $12kg$ .
D. The minimum reading of the machine will be zero.
Correct statements are:

Answer 1

Firstly we will try to draw a diagram for a better understanding of the situation. We will find the mass of the man from the given weight. As the platform is harmonically moving up and down, the maximum weight will be attained while the platform is moving up as the acceleration acting on the body will be due to gravitation and the motion of the platform. The minimum weight will be attained while the platform is moving down. We will find the maximum acceleration attained by the platform by multiplying the amplitude of the harmonic motion with the square of the angular velocity.

Formula used:
$\begin{aligned} & weight=m\times {{a}_{net}} \\\ & {{a}_{\max }}=A\times {{\omega }^{2}} \\\ \end{aligned}$

Complete step by step answer:
We will construct a diagram for understanding the situation.

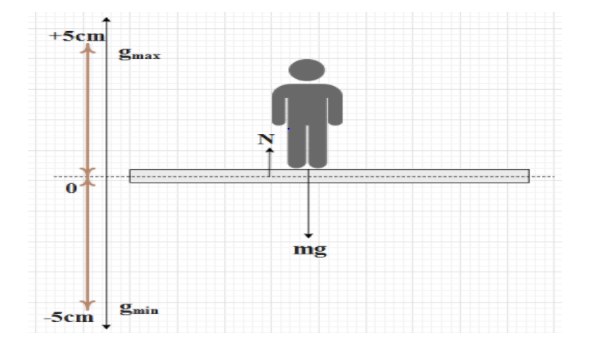
The normal weight of the man is given by$60kg$. Let us find his mass (g=10m/s)
$m=\dfrac{60}{10}=6kg$
So, the mass of the man is $6kg$ .
Now, we will find the maximum acceleration gained by the platform while the harmonic motion.

& {{a}_{\max }}=A\times {{\omega }^{2}} \\\ & \Rightarrow {{a}_{\max }}=A\times {{\left( 2\pi \upsilon \right)}^{2}} \\\ \end{aligned}$$ $${{a}_{\max }}=0.05\times {{\left( 2\times 3.14\times 2 \right)}^{2}}=7.88m/{{s}^{2}}$$ Now, we will find the maximum reading shown by the machine. The maximum weight will be attained while the platform moves upwards as the acceleration due to gravity changes to $$g+{{a}_{\max }}$$ . Then the machine will read the maximum weight as, $${{w}_{\max }}=m\left( g+{{a}_{\max }} \right)=6\left( 10+7.88 \right)=107.28kg$$ So the maximum weight will be nearly equal to $$108kg$$ . Now, the machine will read minimum weight when the platform is moving downwards as the acceleration due to gravity becomes $$g-{{a}_{\max }}$$ . Then, the minimum weight read by the machine will be, $${{w}_{\min }}=m\left( g-{{a}_{\max }} \right)=6\left( 10-7.88 \right)=12.72kg$$ So the minimum weight read by the machine is nearly $$12kg$$ . We will conclude the solution as the maximum weight read by the weighing machine is $$108kg$$ and the minimum weight is nearly $$12kg$$ . So we have two correct statements here. That is both option A and option C are correct. **Note:** This question resembles the exact condition when a person is standing in an elevator. In an elevator, we will feel as our weight increases when it is moving upwards. This is due to the increase in net acceleration on our body mass. Similarly, we will feel weight reduced while the elevator is moving downwards as the net acceleration reduces. Another important point is we must take the maximum acceleration of the platform to get maximum and minimum readings in the weighing machine.