Question
Question: A person moves 30 m north and then 20 m towards east and finally \(30\sqrt{2}\) m in south-west dire...
A person moves 30 m north and then 20 m towards east and finally 302 m in south-west direction. The displacement of the person from the origin will be
A
10 m along north
B
10 m long south
C
10 m along west
D
Zero
Answer
10 m along west
Explanation
Solution
From figure, OA→=06mui→+306muj→, AB→=206mui→+06muj→
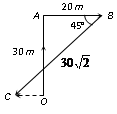
BC→=−3026mucos45oi→−3026musin45oj→ =−306mui→−306muj→
∴ Net displacement, OC→=OA→+AB→+BC→=−106mui→+06muj→
∣OC→∣6mu=106mum.
