Question
Question: A person is moving in a circle of radius r with constant speed v. The change in velocity in moving f...
A person is moving in a circle of radius r with constant speed v. The change in velocity in moving from A to B is
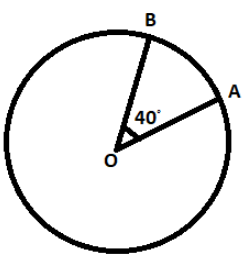
Solution
We can find the change in velocity of the person while moving from point A to B using the cosine law of vector considering the angle between the velocity vectors as 40∘. Since, the velocity of the person will be constant, the value of velocity at both the points will be the same. And, accordingly we need to find the resultant of the two vectors considering the given angle which will be the value of change in velocity.
Complete step by step answer:
To solve this question we need to understand the meaning of vector and uniform circular motion.Vector means a quantity which has both direction and magnitude. There are many different types of vector like null vector, parallel vector, antiparallel vector, orthogonal vector.
Accordingly, the resultant of two vectors can be found using the cosine law of vectors.i.e. R=P2+Q2−2PQcosθ ; where P and Q are two different vectors.Uniform circular motion is a motion in which a body moves around a fixed point or on a circular track with uniform speed. When an object is in uniform circular motion, its speed doesn't change during its complete cycle.
Now let v1 and v2 be the velocities of the person at point A and B respectively.Since, the speed of person ∣v∣ is constant.Therefore, ∣v1∣=∣v2∣=v
Now since ∠AOB=40∘ , therefore the angle between the velocity vectors is also 40∘.
Now, change in vector (Δv)=v2−v1
And, ∣Δv∣=∣v2∣2+∣v1∣2−2v2v1Cosθ
Δv=v2+v2−2vvcos40o
⇒Δv=2v2−2v2cos40o
⇒Δv=2v2(1−cos40o)
Now, since cos40∘=1−2sin220∘
Hence, Δv=2v2(1−(1−2sin220∘)
Δv=2v2(1−1+2sin220∘)
⇒Δv=2v2(2sin220∘)
⇒Δv=4v2sin220∘)
∴Δv=2vsin20∘
Hence, the magnitude of change in velocity in moving from point A to B is 2vsin20∘.
Note: The Law of Cosines is used to calculate the magnitude (r) and the Law of Sines is used to calculate the angle (α) of two vectors. Hence, don’t confuse between the two laws and apply accordingly. The value obtained using the Law of Cosines is the resultant of the two vectors and its direction is decided accordingly depending on the direction of the two vectors.
