Solveeit Logo
Login

Question

Question: A person is drawing himself up and a trolley on which he stands with some acceleration. Mass of the ...

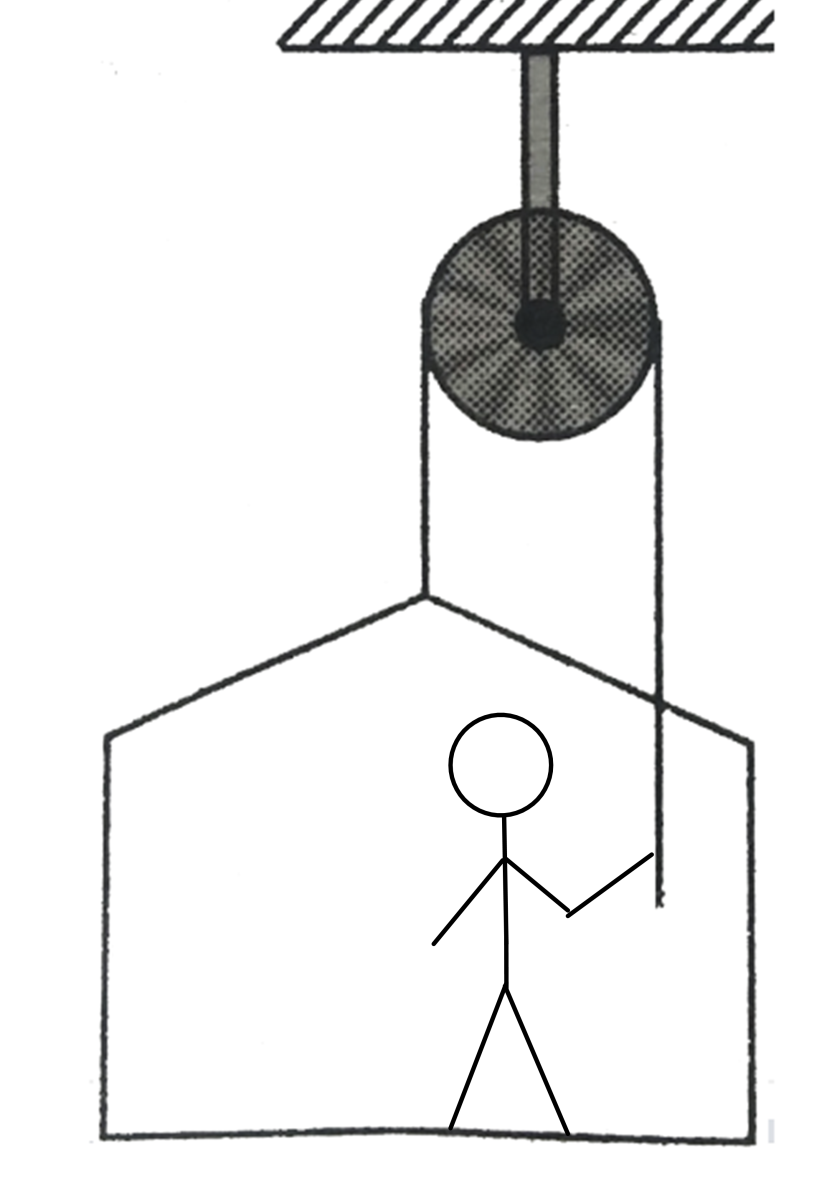
A person is drawing himself up and a trolley on which he stands with some acceleration. Mass of the person is more than the mass of the trolley. As the person increases his force on the string, the normal acceleration between person and the trolley will

(A) Increase
(B) Decrease
(C) Remain same
(D) Cannot be predicted as data is insufficient

Explanation

Solution

To solve this problem, find the equation of motion using Newton’s second law for the trolley and the person in it then solve for the normal force acting on it to find the normal acceleration. Newton’s second law states that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object. It can be written as, F=maF = ma .

Complete step by step answer:
We have here a person in a trolley going up with some acceleration.
Let's assume that, the mass of the person is mm , mass of the trolley is MM , Normal force by the floor of the trolley is NN . Acceleration of the trolley aa and is the tension in the rope TT that is the force exerted by the man also.

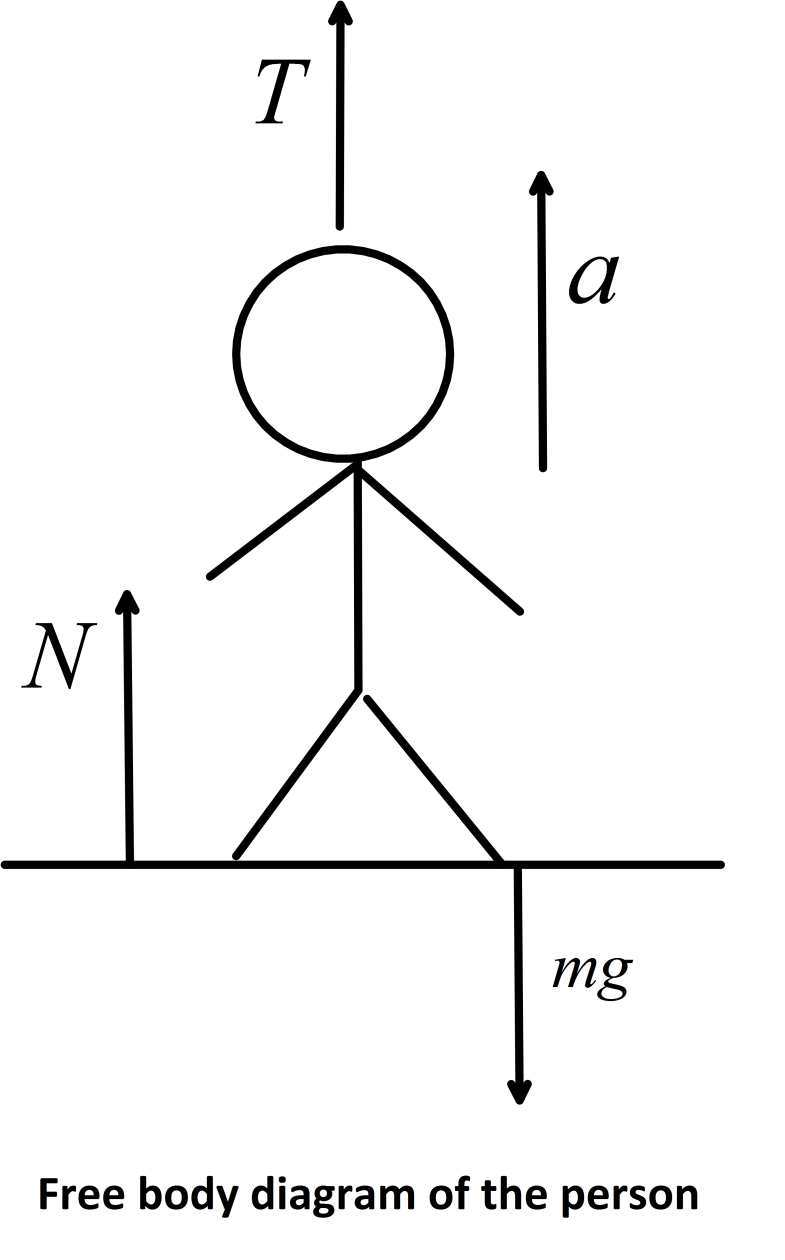
So, equation of motion of the man can be written as,
T+N−mg=maT + N - mg = ma
Or, T+N=m(a+g)T + N = m(a + g) ….(i)

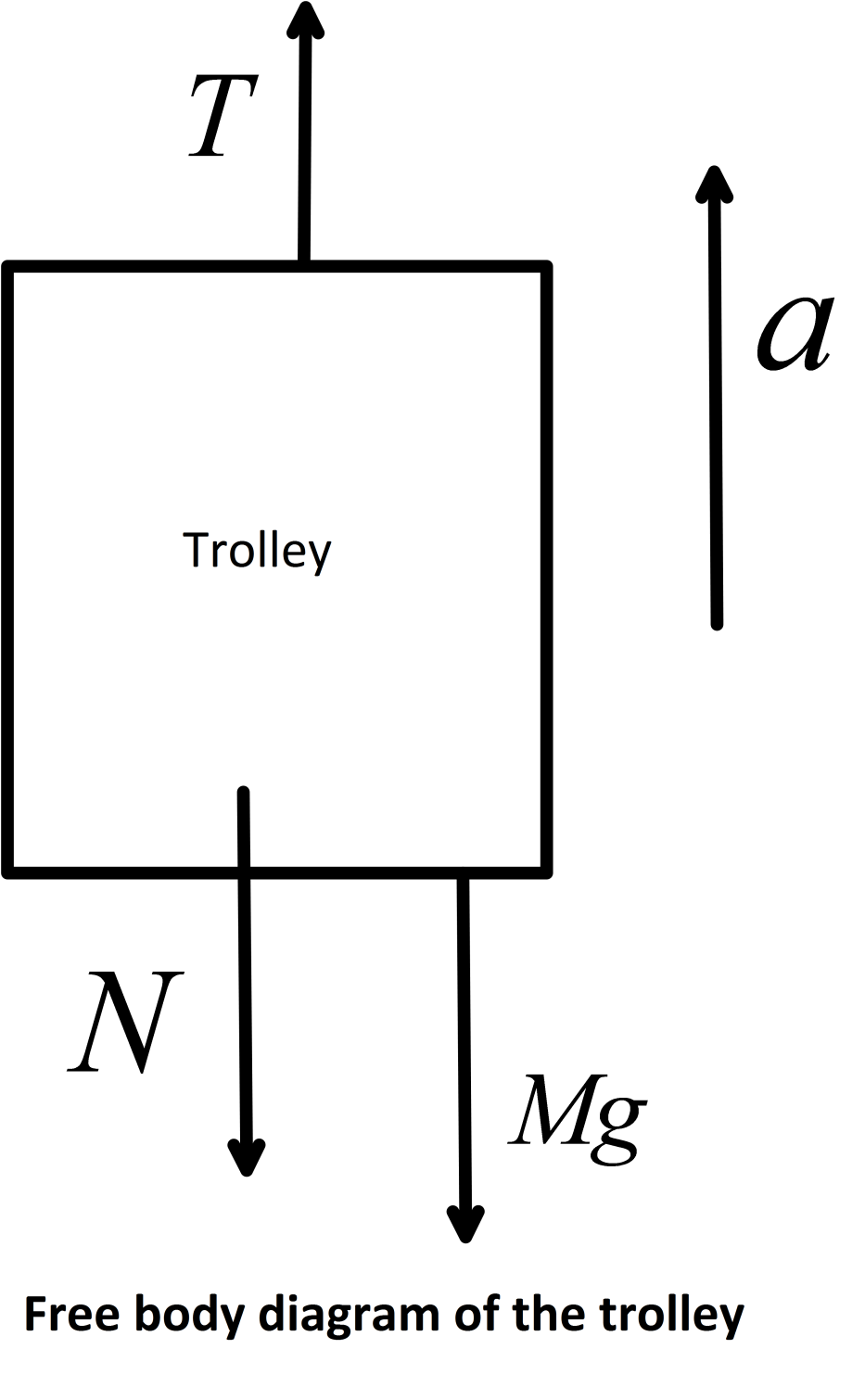
We can write the equation of motion of the trolley as,
T−N−Mg=MaT - N - Mg = Ma
Or, T−N=M(g+a)T - N = M(g + a) …..(ii)
Hence, Dividing equation (i) and (ii) we get,
T+NT−N=mM\dfrac{{T + N}}{{T - N}} = \dfrac{m}{M}
Simplifying we get,
TN=m+Mm−M\dfrac{T}{N} = \dfrac{{m + M}}{{m - M}}
So, T∝NT \propto N since the mass of the trolley and the person is fixed.
Since, the person is increasing the force on the string so the tension on the string will increase, the normal acceleration will also increase.
So, option (A) is correct.

Note:
Tension on the string is proportional to the acceleration of the trolley/person so the normal acceleration is also proportional to the normal acceleration. If the acceleration of the trolley/person increases then normal acceleration also increases. So, the person has to exert more force on the string.