Question

A person intending to cross a river by the shortest path starts at an angle Alpha with the downstream of the speed of the person less than that of the water current show that Alpha must be obtuse.

Answer 1

- Hint: In this case, the shortest path is not the shortest distance between two ends of the banks of the river i.e. width of the river. You have to consider the force acting on the swimmer by flowing water in the river. Resolve the velocity vector of the person into its horizontal and vertical components.

Complete step-by-step solution

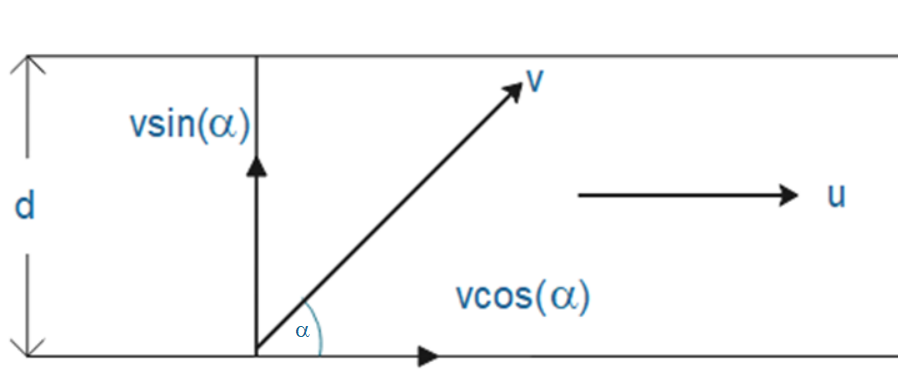
Let u be the velocity of water flowing in the river of width d. Let v be the velocity of the person swimming at an angle of ∝ in river from downstream.
Now resolve v into its horizontal and vertical components which are $v\cos \alpha$ and $v\sin \alpha$respectively.
Total time taken by the person to cross the river is given by,
$\begin{aligned} & Time\text{ }=\text{ }\dfrac{displacement}{velocity} \\\ & t=\dfrac{d}{v\sin \alpha } \\\ \end{aligned}$
Let x be the total distance covered by the person in downstream, which is given by,
$x=\left( u+v\cos \alpha \right)\dfrac{d}{v\sin \alpha }$
We can eliminate ∝ by using the values of $\sin \alpha$and $\cos \alpha$.
We have,
$\sin \alpha =\dfrac{d}{tv}\text{ and }\cos \alpha =\dfrac{\sqrt{{{t}^{2}}{{v}^{2}}-{{d}^{2}}}}{tv}$
Substituting these values in the above equation, we get,
${{t}^{2}}({{u}^{2}}-{{v}^{2}})-2xvt+({{x}^{2}}-{{\alpha }^{2}})=0$
We know that should have real solutions, thus, discernment should be greater than or equal to zero.
Therefore,
$4{{x}^{2}}{{v}^{2}}\ge 4({{u}^{2}}-{{v}^{2}})({{x}^{2}}+{{d}^{2}})$
$x\ge \dfrac{d}{v}(\sqrt{{{u}^{2}}-{{v}^{2}}})$
For the shortest path time must be least. So again time is given by,
$t=\dfrac{d}{v\sin \alpha };x=\dfrac{d}{v}\sqrt{({{u}^{2}}-{{v}^{2}})}=\dfrac{d}{v\sin \alpha }(u+v\cos \alpha )$

& ({{u}^{2}}-{{v}^{2}}){{\sin }^{2\alpha }}={{(u+v\cos \alpha )}^{2}} \\\ & {{u}^{2}}(1-{{\sin }^{2}}\alpha )+2uv\cos \alpha +{{v}^{2}}=0 \\\ & \text{After solving, we get,} \\\ & \cos \alpha =-\dfrac{u}{v} \\\ \end{aligned}$$ Since the cosine of the angle is negative, the angle must be obtuse. Hence proved. **Note:** Note that vector quantities can be resolved into their horizontal and vertical components. Also, remember that the cosine of an obtuse angle is negative and if the angle is acute then its cosine is positive. Do not get confused between the speed and velocities, they are two different quantities. Speed is a scalar quantity while velocity is a vector quantity. The magnitude of speed and velocity are the same.