Question

A person in a wheelchair is moving up a ramp at constant speed. Their total weight is 900N. The ramp makes an angle of ${{37}^{\circ }}$ with the horizontal. Calculate the component of its weight parallel and perpendicular to the ramp.

A. Component of weight parallel to ramp is ${{W}_{||}}=900\sin {{37}^{\circ }}$. Component of weight perpendicular to ramp is ${{W}_{\bot }}=900\cos {{37}^{\circ }}=520N$
B. Component of weight parallel to ramp is ${{W}_{||}}=900\sin {{37}^{\circ }}$. Component of weight perpendicular to ramp is ${{W}_{\bot }}=900\cos {{37}^{\circ }}=720N$
C. Component of weight parallel to ramp is ${{W}_{||}}=900\sin {{37}^{\circ }}$. Component of weight perpendicular to ramp is ${{W}_{\bot }}=900\cos {{37}^{\circ }}=420N$
D. Component of weight parallel to ramp is ${{W}_{||}}=900\sin {{37}^{\circ }}$. Component of weight perpendicular to ramp is ${{W}_{\bot }}=900\cos {{37}^{\circ }}=320N$

Answer 1

Weight of the body is equal to the gravitational force exerted on it. The gravitational force acting on a body is always in downward direction. Resolve the gravitational force into its components along the plane and perpendicular to the plane of the ramp.

Complete step by step answer:
Weight of a body is the force by which the earth pulls the body towards itself due to gravity. This means that the weight of the body is equal to the gravitational force exerted on it. On the surface of earth, the gravitational force is always directed downwards, i.e. in the direction of the negative y-axis. It is given that the weight of the man and the wheelchair is equal to 900N. Therefore, the vector of the weight can be drawn as shown in the figure below.

It is said that the man is travelling at a constant speed on a ramp, which is inclined by an angle of ${{37}^{\circ }}$ with the horizontal. This means that the plane of the ramp makes an angle of ${{37}^{\circ }}$ with the positive x-axis (as shown).

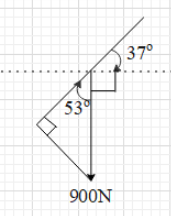
From the figure, we get that the angle between the plane and the weight is ${{53}^{\circ }}$.
Therefore, the component of the weight parallel to the plane is ${{W}_{||}}=900\cos {{53}^{\circ }}$ and the component perpendicular to the plane is ${{W}_{\bot }}=900\sin {{53}^{\circ }}$.
We know that $\cos \theta =\sin \left( {{90}^{\circ }}-\theta \right)$ and $\sin \theta =\cos \left( {{90}^{\circ }}-\theta \right)$.
$\cos {{53}^{\circ }}=\sin \left( {{90}^{\circ }}-{{53}^{\circ }} \right)=\sin {{37}^{\circ }}$
And $\sin {{53}^{\circ }}=\cos \left( {{90}^{\circ }}-{{53}^{\circ }} \right)=\cos {{37}^{\circ }}$.
Now, we can write that ${{W}_{||}}=900\sin {{37}^{\circ }}$ and ${{W}_{\bot }}=900\cos {{37}^{\circ }}$.
And $\cos {{37}^{\circ }}=\dfrac{4}{5}$.
$\therefore {{W}_{\bot }}=900\times \dfrac{4}{5}=720N$.
Therefore, the component of weight parallel to ramp is ${{W}_{||}}=900\sin {{37}^{\circ }}$ and component of weight perpendicular to ramp is ${{W}_{\bot }}=720N$.

Hence, the correct option is B.

Note: If two angles x and y are such that their sum is equal to 90 degrees,
i.e.$x+y={{90}^{\circ }}$, then the two are said to be complementary angles. In this case, the angles ${{37}^{\circ }}$ and ${{53}^{\circ }}$ are complementary to each other.Weight is not anything but the force gravity experiences. It is represented by W and Newton is its SI unit. It is articulated as the product of mass and acceleration due to gravity. So the weight of a given object will show variation according to the gravity in that particular space.