Question

A person draws water from a $5m$ deep well and bucket of mass $2kg$ of capacity $8litre$ by a rope of mass $1kg$ . What is the total work done by the person? $\left( {{\text{Assume}}\,\,g = 10m/{{\sec }^2}} \right)$

Answer 1

Work is said to be done on a body by a force, when the force acting on the body produces a displacement in any direction except in a direction perpendicular to direction of force. It measures the energy transfer that takes place. Work is a scalar product. There are positive work done, negative work done and zero work done.
Formula:
Work done,
$W = F \cdot S$
Where
$F$ , is the force
And $S$ , is the displacement
Force can be written as $f = mg$
Where $m$ , is the mass of body and $g$ is the acceleration of body

Complete Step by Step Answer:
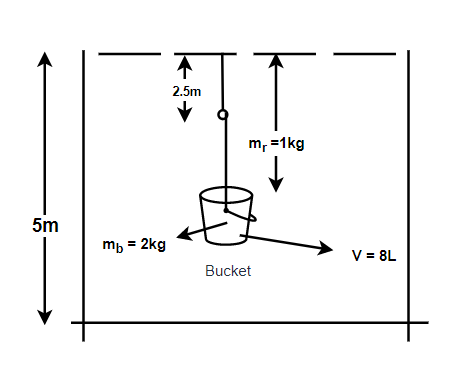
According to question, the height of well, $h = 5cm$ , Mass of bucket, ${m_b} = 2kg$ , Mass of rope, ${m_r} = 1kg$ and Volume of bucket, $V = 8litre$

We know that, Density of water is $1000kg{m^{ - 3}}$ or $1gc{m^{ - 3}}$
As density = mass/ volume
To convert liters to kilogram, we will use above formula of density to calculate mass of water in $kg$ which is ${\text{Mass}}\,\,{\text{ = }}\,\,{\text{Density \times Volume}}$
$\Rightarrow 1\dfrac{{kg}}{{{m^3}}} \times 8{m^3} = 8kg$
Mass of water is equal to $8kg$
Total mass of bucket and water, $m = \left( {8 + 2} \right)kg = 10kg$
So, Total work done $\left( w \right)$ will be equal to, Work done to lift bucket ${W_o}$ and the addition of Work done to lift rope ${W_r}$
Work done to lift bucket, ${W_ \circ } = Mgh = 10 \times 10 \times 5 = 500J$
As use know that work done to lift rope will depend on Centre of mass of rope which is at $2.5m$
(We must consider the bucket to be of negligible height)
Then, only the Centre of mass of rope will lie at $2.5m$ which is half the height.
Work done to lift rope $\left( {{W_r}} \right) = {M_r}g\dfrac{h}{2} = 1 \times 10 \times 2.5 = 25J$
So, total work done, $W = 500 + 25 = 525J$

Therefore, option $\left( b \right)$ is correct answer

Note: The unit of work done is Joule $\left( J \right)$ . Also, if more than one force is acting on a body, the work done by all the forces together is the sum of work done by each of them separately.