Question

A person can see things clearly up to $3{\text{m}}$. What is the power of the lens he should use so that he can see up to $12{\text{m}}$ ?

Answer 1

Since the person can see the object placed at $3m$ which means that is his far point. We will use a lens whose power is so much that it can make an object at $12m$ appear to be at $3m$so it appears clearly to the person. By using lens formula and power of a lens formula we will find our required power of lens.

Complete answer:
We need to find the power of the lens which is required to increase the long-distance sight of the person.

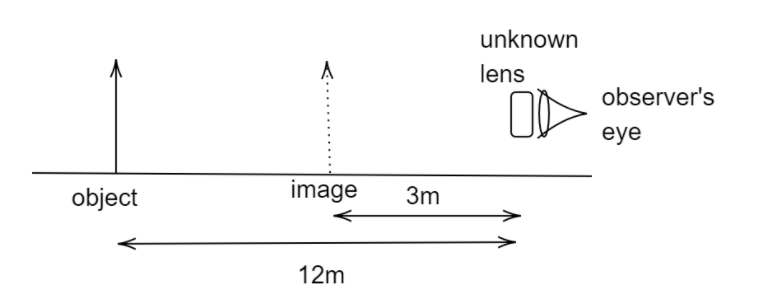
Let the distance between the object and the person be represented by $u$
And the distance between the image formed and the person be represented by $v$
We know from the lens formula we have
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Now substituting the values that we have given in the question we get
$\dfrac{1}{{ - 300}} - \dfrac{1}{{( - 1200)}} + = \dfrac{1}{f}$
We converted the image distance and the object distance given into centimetres.
Now calculating the equation for finding the focal length of the lens we get
$f = - 400{\text{cm}}$
The negative sign indicates the nature of the lens. The negative sign of the focal length is because of the negative image distance. The nature of the lens will be the concave lens.
We know that the power is inversely proportional to the focal length of the lens, therefore we get
$P = \dfrac{{100}}{{f({\text{cm}})}}$
Substituting the value of the focal length we get
$P = \dfrac{{100}}{{ - 400}} = - 0.25{\text{D}}$
Hence the power of the required lens is $- 0.25{\text{D}}$.

Note:
The value of distance of object and distance of image is taken as negative as they are placed on the left hand side of the person’s eye. The power of the lens can bend the rays of light to form correct images. The negative sign in a focal length represents that the lens is concave. If the power of the lens is more, the bending of the light is more.