Question

A permanent magnet is shaped as a ring with a narrow gap between the poles. The mean diameter of the ring equals d=20 cm. The width of the gap is equal to b=2.0 mm and that magnetic induction in the gap is equal to B=40 mT. Assuming that the scattering of the magnetic flux at the gap edges is negligible, then the modulus of the magnetic field strength vector inside the magnet is $1.01 \times {10^x}A/m$. Find $x$.

Answer 1

When we place a nonmagnetic material which can be magnetized in an external magnetic field then there will be magnetic property induced in it. One noticeable thing over here is the amount of magnetic strength induced will be greater than the original applied magnetic field. That means the magnetism induction (B) in that material depends upon the intensity of magnetic field(H) and intensity of magnetization(I).

Formula used: $\oint {H.dl = 0}$
$B = {\mu _0}H$

Complete step by step answer:
we are given with the ring whose mean diameter is 20cm and there is the small gap in between the poles whose width is given as 2mm which is denoted as b and the mean diameter is denoted as d. we are also given with the magnetic induction at the gap which is B=40mT. we were asked to find the modulus of magnetic field vector i.e magnetic field intensity(H). since they told modulus we should find only the magnitude of it and not direction.
We will apply maxwell loop law to find out this
Since no current is enclosed with in the ring we can interpret the maxwell loop law as $\oint {H.dl = 0}$

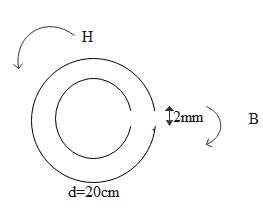
Total length of the ring will be $\pi d$ length of the gap is ‘b’ so effective length of the ring excluding the gap will be $\pi d - b$
We have $B = {\mu _0}H$
We know that $\mu = 4\pi \times 10^{-7}$
Now substituting all the known values on following formula-
From $\oint {H.dl = 0}$ we get
\eqalign{ & H(\pi d - b) + \dfrac{B}{{{\mu _0}}}b = 0 \cr & \Rightarrow H = \dfrac{{ - \dfrac{B}{{{\mu _0}}}b}}{{\pi d - b}} \cr & \Rightarrow H = \dfrac{{\dfrac{{ - 40 \times {{10}^{ - 3}}}}{{4\pi \times {{10}^{ - 7}}}} \times 2 \times {{10}^{ - 3}}}}{{(\pi \times 20 \times {{10}^{ - 2}}) - (2 \times {{10}^{ - 3}})}} \cr & \Rightarrow H = 101A/m \cr & \Rightarrow H = 1.01 \times {10^2}A/m \cr}
So the value of $x$ is 2

Note: Usually this maxwell law is used to find out the magnetic field produced due to the current carrying wire i.e a loop is imagined and we will find out the magnetic field induction at that loop. But here since enclosed current is zero we assume that loop as this ring and hence we equate the integral to zero otherwise it will be a product of permeability and enclosed current.