Question

A perfectly reflecting mirror of mass M mounted on a spring constitutes a spring-mass system of angular frequency Ω such that 4pMΩ/h = ${10^{24}}{m^{ - 2}}$ with h as Planck’s constant, N photons of wavelength λ = $8\pi \times {10^{ - 6}}m$ strike the mirror simultaneously at normal incidence such that the mirror gets displaced by 1 μm. If the value of N is x $\times {10^{12}}$, then the value of x is _______. [Consider the spring as massless]

Answer 1

The radiation when it hits on a surface it will exert some force on the surface. When it hits normally then force is applied normally and if we consider surface and radiation as a system, we can conserve the linear momentum as these forces will be internal forces. Since this surface is connected to spring, it will execute SHM too. Based on these hints one can solve the question.

Formula used:
\eqalign{ & V = A\omega \cr & \Delta p = \dfrac{{2h}}{\lambda } \cr}

Complete step by step answer:
Since the radiation is hitting on the mirror normally there will be change in momentum of the radiation and it is given by $\Delta p = \dfrac{{2h}}{\lambda }$
If the surface is an absorptive surface then the change in momentum of the radiation would be only half of the above value. Since the mirror is a reflective surface we got that value.
The diagram representing the spring and mirror system is given below.

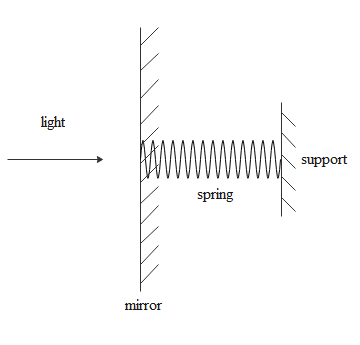
Since mirror is at rest initially, the same momentum will be imparted to the mirror
For N photons it will be
$\Delta p = \dfrac{{2Nh}}{\lambda }$
So the velocity of mirror would be
\eqalign{ & \Delta p = Mv = \dfrac{{2Nh}}{\lambda } \cr & \therefore v = \dfrac{{2Nh}}{{M\lambda }} \cr}
The spring will execute the SHM with the given displacement as an amplitude. So this initial position of mirror would be the mean position. At mean position the velocity will be
\eqalign{ & v = A\Omega = \dfrac{{2Nh}}{{M\lambda }} \cr & \Rightarrow N = \dfrac{{A\Omega M\lambda }}{{2h}} \cr & \Rightarrow \dfrac{{4\pi M\Omega }}{h} = {10^{24}} \cr & \Rightarrow \dfrac{{M\Omega }}{h} = \dfrac{{{{10}^{24}}}}{{4\pi }} \cr & \Rightarrow N = \dfrac{{A\dfrac{{{{10}^{24}}}}{{4\pi }}\lambda }}{2} \cr & \Rightarrow N = \dfrac{{\left( {1 \times {{10}^{ - 6}}} \right){{10}^{24}}(8\pi \times {{10}^{ - 6}})}}{{8\pi }} \cr & \therefore N = 1 \times {10^{12}} \cr}
Hence the value of x will be 1.

Note:
Exactly at the position where radiation hits the surface, that will be the mean position of the oscillation. Then the mirror displaces until the spring force equals the radiation force. So the maximum displacement which the mirror gets due to the radiation will be its amplitude of oscillation and here it is given as 1 micro meter. So we have got the amplitude and the velocity at the mean position, then we can find out the required N value.