Question

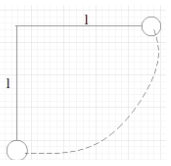
A pendulum with a string of length $l$ is moved up to a horizontal position and released as represented in the diagram. What will be the minimum strength of the string that can overcome the tension as the pendulum is passing through the position of equilibrium when the mass of the pendulum is $m$? (Neglect mass of the string and the air resistance)

$\begin{aligned} & A.mg \\\ & B.2mg \\\ & C.3mg \\\ & D.5mg \\\ \end{aligned}$

Answer 1

First of all analyse the figure. Obtain an expression from it. The square of the velocity of the pendulum will be equivalent to the product of twice the acceleration due to gravity and length of the string of the pendulum. Substitute this in the equation formulated and calculate the tension from it. This will help you in answering this question.

Complete answer:
Using the figure we can write that,
$T-mg=\dfrac{m{{v}^{2}}}{l}$
Where $T$ be the tension in the string, $m$ be the mass of the pendulum, $g$ be the acceleration due to gravity, $v$ be the velocity of the pendulum and $l$ be the length of the pendulum.
The square of the velocity of the pendulum will be equivalent to the product of twice the acceleration due to gravity and length of the string of the pendulum. This can be written as,
${{v}^{2}}=2gl$
So let us substitute this in the above mentioned equation as,
$T=mg\dfrac{m2gl}{l}=3mg$
Hence the tension in the string of the pendulum has been found.

The answer has been obtained as option C.

Note:
A simple pendulum includes a mass which is hanged from a string of some fixed length and this has been placed at a pivot point. When the bob is moved to a certain angle and released, then the pendulum will swing back and forth in a periodic motion. This is known as oscillation. The time period of the simple harmonic motion can be found by taking the product of twice the pi and the square root of the ratio of length and acceleration due to gravity.