Question

A pendulum of mass 1 kg and length $l=1m$ is released from rest at an angle $\theta ={{60}^{\circ }}$. The power delivered by all the forces acting on the bob at angle $\theta ={{30}^{\circ }}$ will be (take $g=10m{{s}^{-2}}$)
A. 13.5 W
B. 20.4 W
C. 24.6 W
D. Zero

Answer 1

power delivered by a force ($\overrightarrow{F}$) is given as $P=\overrightarrow{F}.\overrightarrow{v}=Fv\cos \alpha$ , where $\overrightarrow{v}$ is the velocity of the body and $\alpha$ is the angle between $\overrightarrow{F}$ and $\overrightarrow{v}$. Here, the forces are tension and the gravitational force. Find the velocity of the bob at $\theta ={{30}^{\circ }}$ by using the work energy theorem.

Formula used:
$P=\overrightarrow{F}.\overrightarrow{v}=Fv\cos \alpha$
${{F}_{g}}=mg$
$W={{F}_{g}}h$
$K=\dfrac{1}{2}m{{v}^{2}}$
where $\overrightarrow{v}$ is the velocity of the body and $\alpha$ is the angle between $\overrightarrow{F}$ and $\overrightarrow{v}$.

Complete step by step answer:
There are two forces acting on the bob of the pendulum, the gravitational force exerted by earth and the tension due to the string attached. The direction of the gravitational force (${{F}_{g}}=mg$) is the direction of the negative y-axis (downwards). The direction of the tension (T) is along the length of the string, as shown in the figure.

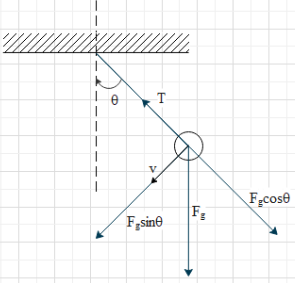
Resolve the gravitational force into its components along the length of the string and perpendicular to the length, as shown. The component of gravitational force along the string is ${{F}_{g}}\cos \theta$ and the component of the gravitational force perpendicular to the length is ${{F}_{g}}\sin \theta$.Now, power delivered by a force ($\overrightarrow{F}$) is given as
$P=\overrightarrow{F}.\overrightarrow{v}=Fv\cos \alpha$ ,
where $\overrightarrow{v}$ is the velocity of the body and $\alpha$ is the angle between $\overrightarrow{F}$ and $\overrightarrow{v}$.
We can see that the tension (T) and force ${{F}_{g}}\cos \theta$ are always perpendicular to the velocity of the bob. Hence, force these two forces $\alpha ={{90}^{\circ }}$.
But $\cos {{90}^{\circ }}=0$. This means that the power delivered by these two forces is zero for all time.
Whereas the force ${{F}_{g}}\sin \theta$ and the velocity of the bob are always parallel.
This means that $\alpha ={{0}^{\circ }}$ and $\cos {{0}^{\circ }}=1$.
$\Rightarrow P=\overrightarrow{F}.\overrightarrow{v}={{F}_{g}}\sin \theta v$

Let us calculate the power delivered by the force ${{F}_{g}}\sin \theta$.
When $\theta ={{30}^{\circ }}$, ${{F}_{g}}\sin \theta =mg\sin {{30}^{\circ }}$.
$\Rightarrow P=mg\sin {{30}^{\circ }}v$ …. (i).
Let us find the velocity of the bob at this position.

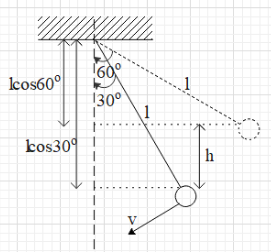
When the bob comes down from $\theta ={{60}^{\circ }}$ to $\theta ={{30}^{\circ }}$, it comes down by a height of $h=l\cos {{30}^{\circ }}-l\cos {{60}^{\circ }}$.
$\Rightarrow h=(1)\dfrac{\sqrt{3}}{2}-(1)\dfrac{1}{2}=\dfrac{\sqrt{3}-1}{2}$.
This means that gravity has done a work equal to $W={{F}_{g}}h=mgh$.
Due to this work done on the bob, its kinetic energy increases to $K=\dfrac{1}{2}m{{v}^{2}}$. Since it started from rest, the change in its kinetic energy is,
$\Delta K=\dfrac{1}{2}m{{v}^{2}}$.
And $W=\Delta K$.
$\Rightarrow mgh=\dfrac{1}{2}m{{v}^{2}}$
Substitute the value of g and h.
$(10)\dfrac{\left( \sqrt{3}-1 \right)}{2}=\dfrac{1}{2}{{v}^{2}}$
$\Rightarrow {{v}^{2}}=(10)\left( \sqrt{3}-1 \right)=7.32$
$\Rightarrow v=2.7m{{s}^{-1}}$.
Substitute the value of v in (i).
$\Rightarrow P=mg\sin {{30}^{\circ }}(2.7)$.
Substitute the known values.
$\Rightarrow P=(1)\left( 10 \right)\left( \dfrac{1}{2} \right)(2.7)=13.5W$.
Therefore, the total power delivered to the bob at angle $\theta ={{30}^{\circ }}$ is equal to 13.5W

Hence, the correct option is A.

Note: The work done by the tension force is zero. This is because work done by a force is defined as the dot product of the applied force and the displacement of the body. However, the dot product of perpendicular vectors is zero and here the tension and the displacement of the bob are perpendicular to each other. We can also find the speed of the bob by law of conservation of mechanical energy.