Question

A pendulum is hanging from the ceiling of a car having an acceleration ${a_0}$ with respect to the road. Find the angle made by the string with the vertical.

Answer 1

Hint Here, we need to know that when the car is accelerated a pseudo force will be acting on the pendulum in the opposite direction. If we analyze all the forces that are acting on the pendulum then we can see that the cosine component of tension is balanced by the force of gravity. And the sine component of tension is balanced by the pseudo force. By using these two equations we can find the value of angle made by the pendulum with the vertical.

Complete step by step answer:
It is given that a pendulum is hanging from the ceiling of a car which is having an acceleration ${a_0}$. We need to find the angle which the string makes vertically.
Since it is given that the car is under acceleration, there will be the presence of a pseudo force.
Whenever there is an acceleration of the frame then it should be considered as a non-inertial frame. So, there will be the presence of a pseudo force acting opposite to the direction of acceleration of the frame.
Now let us consider all the forces that are acting on the pendulum.
Considered the diagrammatic representation of the situation shown below.

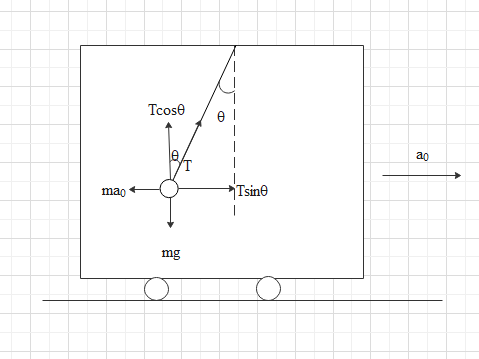
$\theta$ is the angle made by the pendulum with the vertical, Tension in the string is represented as T, $m\,g$ is the force due to gravity, $m{a_0}$ is the pseudo force
There is a force of tension acting on the string. Since it is making an $\theta$ with the vertical we can split the component of tension into $T\sin \theta$ and $T\cos \theta$. Where, $T\cos \theta$ is the component of tension acting along the vertical and $T\sin \theta$ is the component along the horizontal direction.
The force due to gravity $m\,g$ acts directly downwards.
From the figure we can see that the force due to gravity is balanced by the cosine component of tension. That is
$T\cos \theta = mg$.....................(1)
The pseudo force $m{a_0}$ is balanced by the sine component of tension. That is,
$T\sin \theta = m{a_0}$......................(2)
We need to find the angle $\theta$ with the vertical.
For finding this let us divide the above two equations.
Then we get
$\dfrac{{T\cos \theta }}{{T\sin \theta }} = \dfrac{{mg}}{{m{a_0}}}$
$\Rightarrow \tan \theta = \dfrac{g}{{{a_0}}}$
From this we get $\theta$ as,
$\theta = {\tan ^{ - 1}}\dfrac{g}{{{a_0}}}$
This is the angle made by the pendulum with the vertical.

Note: Always remember that whenever there is an acceleration in the frame then it is considered as a non-inertial frame. If the frame is not accelerated, then it is an inertial frame. In the case of a non-inertial frame there will always be the presence of pseudo force which is acting in the direction opposite to the direction of acceleration of the frame.