Question

A pendulum clock gives correct time at 20°C at a place where g = 9.800 m/s². It is taken to a place where g = 9.788 m/s². If it will give correct time at temperature 'T' kelvin. Write the value of $\frac{T-11}{60}$ in OMR sheet.

Coefficient of linear expansion of pendulum = 12 x 10⁻⁶/°C.

Answer 1

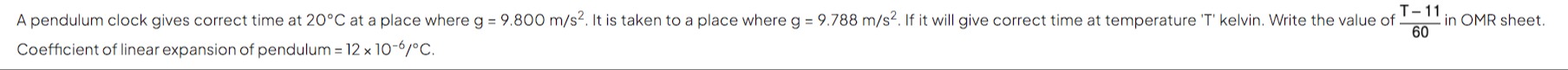
3

Answer 2

The time period of a simple pendulum is given by $T = 2\pi \sqrt{\frac{L}{g}}$. For the pendulum clock to give correct time, its time period must be constant.

Let $T_1 = 20^\circ C$ and $g_1 = 9.800 \, m/s^2$. Let the length of the pendulum at $T_1$ be $L_1$. The time period is $T_1 = 2\pi \sqrt{\frac{L_1}{g_1}}$.

The clock is moved to a place where $g_2 = 9.788 \, m/s^2$. The temperature is $T$ Kelvin. Let the temperature in Celsius be $T_C = T - 273$. The length of the pendulum at temperature $T_C$ is $L_2$. The relationship between $L_1$ and $L_2$ due to thermal expansion is $L_2 = L_1 (1 + \alpha (T_C - T_1))$, where $\alpha$ is the coefficient of linear expansion. The time period at the new location and temperature is $T_2 = 2\pi \sqrt{\frac{L_2}{g_2}}$.

For the clock to give correct time, the time period must remain the same, i.e., $T_1 = T_2$. $2\pi \sqrt{\frac{L_1}{g_1}} = 2\pi \sqrt{\frac{L_2}{g_2}}$ Squaring both sides, we get $\frac{L_1}{g_1} = \frac{L_2}{g_2}$. Substitute $L_2 = L_1 (1 + \alpha (T_C - T_1))$: $\frac{L_1}{g_1} = \frac{L_1 (1 + \alpha (T_C - T_1))}{g_2}$ Assuming $L_1 \neq 0$, we can cancel $L_1$: $\frac{1}{g_1} = \frac{1 + \alpha (T_C - T_1)}{g_2}$ $g_2 = g_1 (1 + \alpha (T_C - T_1))$ $\frac{g_2}{g_1} = 1 + \alpha (T_C - T_1)$ $\frac{g_2}{g_1} - 1 = \alpha (T_C - T_1)$ $\frac{g_2 - g_1}{g_1} = \alpha (T_C - T_1)$ $T_C - T_1 = \frac{g_2 - g_1}{\alpha g_1}$

Given values: $T_1 = 20^\circ C$ $g_1 = 9.800 \, m/s^2$ $g_2 = 9.788 \, m/s^2$ $\alpha = 12 \times 10^{-6} \, /^\circ C$

$T_C - 20 = \frac{9.788 - 9.800}{(12 \times 10^{-6}) \times 9.800}$ $T_C - 20 = \frac{-0.012}{12 \times 10^{-6} \times 9.8}$ $T_C - 20 = \frac{-12 \times 10^{-3}}{12 \times 10^{-6} \times 9.8}$ $T_C - 20 = \frac{-10^{-3}}{10^{-6} \times 9.8} = \frac{-10^3}{9.8} = -\frac{1000}{9.8}$

To get the temperature in Kelvin $T$, we use $T = T_C + 273$. $T = \left(20 - \frac{1000}{9.8}\right) + 273$ $T = 293 - \frac{1000}{9.8}$

We need to calculate the value of $\frac{T-11}{60}$. $\frac{T-11}{60} = \frac{\left(293 - \frac{1000}{9.8}\right) - 11}{60}$ $\frac{T-11}{60} = \frac{282 - \frac{1000}{9.8}}{60}$

$\frac{T-11}{60} = \frac{282 - 102.04}{60}$ $\frac{T-11}{60} = \frac{180}{60} = 3$

Therefore, $\frac{T-11}{60} = 3$.