Solveeit Logo
Login

Question

Question: A pendulum bob of mass \( 80\;mg \) and carrying a charge of \( 4 \times {10^{ - 8}}C \) is at rest ...

A pendulum bob of mass 80  mg80\;mg and carrying a charge of 4×10−8C4 \times {10^{ - 8}}C is at rest in a horizontal uniform electric field of magnitude 20000V/m20000V/m . The tension in the thread of the pendulum and the angle it makes with the vertical is
Acceleration due to gravity g=10ms−2g = 10m{s^{ - 2}}
(A) 82×10−4N,4508\sqrt 2 \times {10^{ - 4}}N,{45^0}
(B) 8×10−4N,6008 \times {10^{ - 4}}N,{60^0}
(C) 62×10−4N,3006\sqrt 2 \times {10^{ - 4}}N,{30^0}
(D) 6×10−4N,3706 \times {10^{ - 4}}N,{37^0}

Explanation

Solution

The mass of the bob of the simple pendulum is given as 80  mg80\;mg . The bob has a charge 4×10−8C4 \times {10^{ - 8}}C in a uniform electric field of magnitude 20000V/m20000V/m . There will be a tension in the thread of the pendulum due to the weight of the bob and the force due to the charged bob in an electric field. We have to find the possible tension on the pendulum and the angle it makes.

Complete Step by step solution

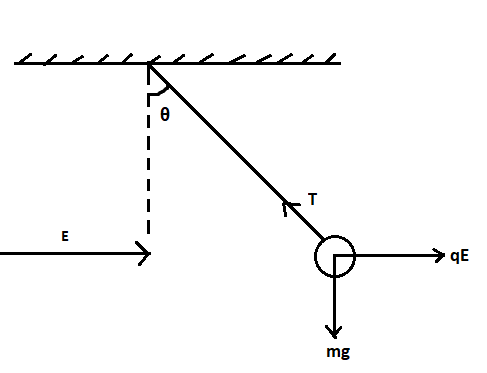
The force on the bob due to gravity can be written as   mg\;mg
The force on the bob due to the electric field can be written as q  Eq\;E
Let TT be the tension on the thread.
The vertical component of the tension Tsin⁡θ=mgT\sin \theta = mg
The horizontal component of the tension Tcos⁡θ=qET\cos \theta = qE
From the two equations, we can write,
T=(mg)2+(qE)2T = \sqrt {{{\left( {mg} \right)}^2} + {{\left( {qE} \right)}^2}}
The mass of the bob is given as m=80mgm = 80mg
The acceleration due to gravity g=10ms−2g = 10m{s^{ - 2}}
The charge on the bob q=4×10−8Cq = 4 \times {10^{ - 8}}C
The magnitude of the electric field E=20000V/mE = 20000V/m
Substituting these values in the above equation,
T=(80×10−6×10)2+(4×10−8×2×104)2T = \sqrt {{{\left( {80 \times {{10}^{ - 6}} \times 10} \right)}^2} + {{\left( {4 \times {{10}^{ - 8}} \times 2 \times {{10}^4}} \right)}^2}}
Solving we get
T=82×10−4NT = 8\sqrt 2 \times {10^{ - 4}}N
The angle between the two components mg  mg\; and qE  qE\; is θ\theta
θ\theta can be written as
tan⁡θ=qEmg\tan \theta = \dfrac{{qE}}{{mg}}
Substituting the values, we get
tan⁡θ=4×10−8×2×10480×10−6×10=1\tan \theta = \dfrac{{4 \times {{10}^{ - 8}} \times 2 \times {{10}^4}}}{{80 \times {{10}^{ - 6}} \times 10}} = 1
tan⁡θ=1\tan \theta = 1
From this,
⇒θ=450\Rightarrow \theta = {45^0}
The answer is: Option (A): 82×10−4N,4508\sqrt 2 \times {10^{ - 4}}N,{45^0} .

Additional information
An oscillating body comes to rest after making some oscillations. This is due to the resistance of air. Such oscillations are called damped oscillations.

Note
The time period of the oscillation of a pendulum does not depend on the mass of the bob. When a body is allowed to oscillate freely it will oscillate with a particular frequency. Such oscillations are called free oscillations. The frequency of free oscillations is called natural frequency. A pendulum that is adjusted in a way that it has a period of two seconds is called a second’s pendulum.