Question

A peacock is sitting on the tree and observes its prey on the ground. It makes an angle of depression of $22{}^\circ$ to catch the prey. The shadow of the peacock was observed to be $10km/hr$ and it catches its prey in $\text{1 min 12 seconds}$ . At what height was the peacock on the tree? $\left( \cos 22{}^\circ =0.927,\sin 22{}^\circ =0.374,\tan 22{}^\circ =0.404 \right)$

Answer 1

Hint : First we draw a diagram, then we find the distance travelled by the peacock to catch the prey as given that the shadow of the peacock was observed to be $10km/hr$ and it catches its prey in $\text{1 min 12 seconds}$ . Then, use this distance as the length of a side of the triangle and use trigonometric property to find the height of the tree.

Complete step-by-step answer :
We have given that a peacock is sitting on the tree and observes its prey on the ground. It makes an angle of depression of $22{}^\circ$ to catch the prey.
Now, let’s draw a diagram by using the given information.

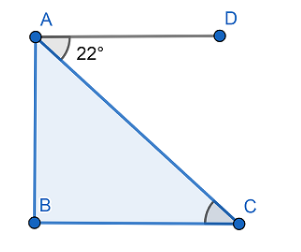
We have to find the height of the tree $AB$.
Let us assume that peacock is sitting at the point $A$ and prey is on the ground at point $C$ . Now, as given in the question It makes an angle of depression of $22{}^\circ$ to catch the prey so $\angle CAD=22{}^\circ$.
Also, $\angle ACB=22{}^\circ$ as $\angle CAD$ and $\angle ACB$ are alternate angles and angle of depression is equal to angle of elevation.
Also, it is given that the shadow of the peacock was observed to be $10km/hr$ and it catches its prey in $\text{1 min 12 seconds}$. A peacock travels a path $AC$ to reach the prey, so the distance travelled by the peacock to reach the prey will be calculated by using the formula $\text{Speed=}\dfrac{\text{Distance}}{\text{Time}}$
We have given the speed of the peacock is $10km/hr$ and time taken to reach the prey is $\text{1 min 12 seconds}$ .
Then, distance will be $\text{Distance=speed}\times \text{time}$
$\text{Distance=}10km/hr\times \text{1 min 12 seconds}$
Now, we have to convert the units. We know that
$\begin{aligned} & 1\text{ minute = 60 seconds} \\\ & \text{1 km/hr = }\dfrac{5}{18}m/\sec \\\ \end{aligned}$
So, we get
$\begin{aligned} & \text{Distance=}\left( 10\times \dfrac{5}{18} \right)\times \left( 60+\text{12} \right) \\\ & \text{Distance}=\dfrac{50}{18}\times 72 \\\ & \text{Distance}=200\text{ m} \\\ \end{aligned}$
In the figure drawn the length of $AC=200$
Now, let us consider right angle triangle $\Delta ABC,$
We know that $\sin \theta =\dfrac{\text{Perpendicular}}{\text{hypotenuse}}$
We have $\theta =22{}^\circ$ , substituting the values we get
$\begin{aligned} & \sin \theta =\dfrac{\text{AB}}{\text{AC}} \\\ & \sin 22{}^\circ =\dfrac{AB}{200} \\\ \end{aligned}$
Now, we have given in the question $\sin 22{}^\circ =0.374$
$\begin{aligned} & 0.374=\dfrac{AB}{200} \\\ & 0.374\times 200=AB \\\ & AB=74.8 \\\ \end{aligned}$
So, the height of the tree is $74.8\text{ m}$ .

Note : The point to remember is that always keep the units the same for all variables. If units are not the same you have to convert the units. In this particular question one may be confused after reading the line that the shadow of the peacock was observed to be $10km/hr$ and it catches its prey in $\text{1 min 12 seconds}$ . But use this line to get the value of a side of the triangle, so you can use it to solve the trigonometric ratio and obtain an answer.