Question

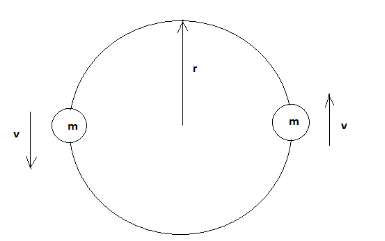
A particular binary star system consists of two identical stars orbiting a point halfway between them along the same circular path at constant speeds (See diagram below). If we call the mass of each star $m$ and the radius of the circular path $r$. What is an expression for the speed of the stars, in terms of these symbols and fundamental constants?

(A) $v = \sqrt {\dfrac{{Gm}}{{2r}}}$
(B) $v = \sqrt {\dfrac{{2Gm}}{r}}$
(C) $v = \sqrt {\dfrac{{Gm}}{r}}$
(D) $v = \sqrt {\dfrac{{Gm}}{{4r}}}$

Answer 1

Since, the two bodies are moving around a fixed orbit, we will find the centripetal force. Again, the two bodies have gravitational force on their own, so we will also find the gravitational force between them. We will equate the two forces followed by manipulation to obtain the expression for velocity.

Complete step by step answer:
In the given question, we are supplied with the following data:
A particular binary star system consists of two identical stars orbiting a point halfway between them along the same circular path at constant speeds.
The speed of both the stars are taken to be $v$ and the mass of each star be $m$ .
The radius of the orbit is taken as $r$ .
We are asked to find the expression for the speed of the stars, in terms of these symbols and fundamental constants.
To begin with, we will take into account the centripetal force which is associated with a body moving around a fixed orbit in space.
The centripetal force is equal to the gravitational force associated with the two heavenly bodies i.e. here in the case are stars.
The centripetal force is given by the expression which is given below:
${F_{\text{c}}} = \dfrac{{m{v^2}}}{r}$ …… (1)
Where,
${F_{\text{c}}}$ indicates the centripetal force associated with the two bodies.
$m$ indicates the mass of each of the stars.
$v$ indicates the velocity at which they are moving.
$r$ indicates the radius of the path they are moving around.
Again, we have the expression for the gravitational force which is given by:
${F_{\text{G}}} = G\dfrac{{m \times m}}{{{{\left( {2r} \right)}^2}}}$ ……(2)
Where,
${F_{\text{G}}}$ indicates the gravitational force between the two bodies.
$G$ indicates the universal gravitational constant.
$m$ indicates the mass of each of the stars.
$2r$ indicates the distance of separation between the two bodies which is twice the radius.
Since, the centripetal force is equal to the gravitational force.
So, from equations (1) and (2), we have:
{F_{\text{c}}} = {F_{\text{G}}} \\\ \Rightarrow\dfrac{{m{v^2}}}{r} = G\dfrac{{m \times m}}{{{{\left( {2r} \right)}^2}}} \\\ \Rightarrow\dfrac{{m{v^2}}}{r} = G\dfrac{{m \times m}}{{4{r^2}}} \\\ \Rightarrow{v^2} = G\dfrac{{{m^2}}}{{4r}} \\\
Again, by further simplifying, we get:
{v^2} = G\dfrac{{{m^2}}}{{m \times 4r}} \\\ \Rightarrow {v^2} = G\dfrac{m}{{4r}} \\\ \therefore v = \sqrt {\dfrac{{Gm}}{{4r}}} \\\

Hence, the expression for the speed of the stars, in terms of these symbols and fundamental constants is $\sqrt {\dfrac{{Gm}}{{4r}}}$. Thus,the correct option is D.

Note: While solving this problem, most of the students seem to have confusion regarding the centripetal force and the centrifugal force. In this case, the force is centripetal one. Centripetal force is defined as the force that is required in a curved path to keep an object moving and that is guided inward towards the centre of rotation. The centrifugal force is defined as the apparent force felt by an object travelling in a curved direction, acting outward from the rotation centre. Essentially, these two forces are the two sides of the same coin.