Question

A particle would take time ${t_1}$ to move down a straight tube from the surface of the earth (supposed to be a homogeneous sphere) to its centre. If gravitational acceleration were to remain constant, time would be ${t_2}$. The ratio$\dfrac{{{t_1}}}{{{t_2}}}$:
A) $\dfrac{\pi }{{2\sqrt 2 }}$
B) $\dfrac{\pi }{2}$
C) $\dfrac{{2\pi }}{3}$
D) $\dfrac{\pi }{{\sqrt 3 }}$

Answer 1

A simple harmonic motion is a periodic motion along two extremes and an equilibrium position. The acceleration due to gravity is constant but in this case 1 the acceleration due to gravity is not constant and varies with position.

Complete step by step solution:
It is given that the acceleration of gravity for case 1 is not constant and changes as the position of the body changes but so in the second case the acceleration of the gravity is constant. We need to find the value of the ratio of time taken in case 1 to reach to the centre of the earth to the time taken by the body to reach to the center of the earth for case 2.
Case 1:

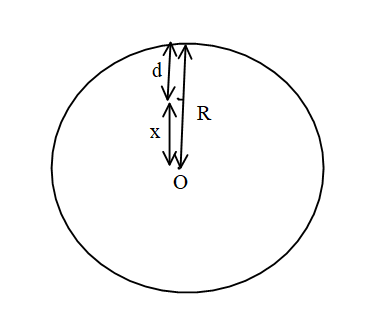
As the acceleration due to gravity changes with position. The acceleration due to gravity can be expressed as,
$g' = g\left( {1 - \dfrac{d}{R}} \right)$
Where $g'$is the new acceleration due to gravity $g$ is the original acceleration due to gravity $d$ is the depth from the surface of the earth and R is the radius of the earth.
Since,
$\Rightarrow g' = g\left( {1 - \dfrac{d}{R}} \right)$
$\Rightarrow g' = g\left( {\dfrac{{R - d}}{R}} \right)$
As $R - d$ is equal to $x$.
$\Rightarrow g' = g\left( {\dfrac{x}{R}} \right)$
Here we see that the acceleration due to gravity is a function of x.
$\Rightarrow g' = F\left( x \right)$
The above relation represents a simple harmonic motion as $g'$ is nothing but acceleration which is a function of distance x.
The revised equation of $g'$ will be equal to
$\Rightarrow g' = - F\left( x \right)$………eq. (1)
The negative sign represents that the motion and the acceleration both are in the opposite direction.
The equation of the acceleration for a simple harmonic motion is given by,
$\Rightarrow a = - x \cdot {\omega ^2}$………eq. (2)
Equating equation (1) and (2) we get,
$\Rightarrow g' = a$
$\Rightarrow - g\left( {\dfrac{x}{R}} \right) = - x \cdot {\omega ^2}$
$\Rightarrow g\left( {\dfrac{x}{R}} \right) = x \cdot {\omega ^2}$
$\Rightarrow \dfrac{g}{R} = {\omega ^2}$
$\Rightarrow \omega = \sqrt {\dfrac{g}{R}}$………eq. (3)
The angular acceleration will be$\omega = \sqrt {\dfrac{g}{R}}$. Therefore the time period will be equal to,
$\Rightarrow T = \dfrac{{2\pi }}{\omega }$
Replace the value of angular velocity from equation (3).
$\Rightarrow T = \dfrac{{2\pi }}{\omega }$
$\Rightarrow T = \dfrac{{2\pi }}{{\sqrt {\dfrac{g}{R}} }}$
As the cycle has four motions and we need the time taken for only one of the motion therefore.
$\Rightarrow {t_1} = \left( {\dfrac{1}{4}} \right)\left( {2\pi \cdot \sqrt {\dfrac{R}{g}} } \right)$
$\Rightarrow {t_1} = \left( {\dfrac{1}{2}} \right)\left( {\pi \cdot \sqrt {\dfrac{R}{g}} } \right)$.........eq. (4)

Case 2:
When acceleration due to gravity is constant.
So the time taken by a body to cross a distance R which is radius of circle.
Apply Newton’s law of motion equation.
$s = u{t_2} + \dfrac{1}{2}a{t_2}^2$
Where s is the distance of travel u is the initial velocity a is the acceleration and ${t_2}$ is the time taken to cross a distance R.
As the initial velocity is zero i.e. $u = 0$ the acceleration due gravity acts on the body $a = g$ and the distance travelled will be$s = R$.
$\Rightarrow s = u{t_2} + \dfrac{1}{2}a{t_2}^2$
Replace the respective values.
$\Rightarrow R = \dfrac{1}{2}g{t_2}^2$
$\Rightarrow {t_2}^2 = \dfrac{{2R}}{g}$
$\Rightarrow {t_2} = \sqrt {\dfrac{{2R}}{g}}$………eq. (5)
Taking ratio of equation (4) to equation (5) we get,
$\Rightarrow \dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{\left( {\dfrac{1}{2}} \right)\left( {\pi \cdot \sqrt {\dfrac{R}{g}} } \right)}}{{\sqrt {\dfrac{{2R}}{g}} }}$
$\Rightarrow \dfrac{{{t_1}}}{{{t_2}}} = \dfrac{\pi }{{2\sqrt 2 }}$
The ratio of the time taken is equal to$\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{\pi }{{2\sqrt 2 }}$.

The correct option for this problem is option A.

Note: The cycle of the body having harmonic motion has four motions. The particle will travel from mean position to one extreme then from one extreme to the mean position again and then from the mean position to another extreme and returns from there to the mean position and this is how it completes one complete cycle.