Solveeit Logo
Login

Question

Question: A particle which is simultaneously subjected to two perpendicular simple harmonic motions are repres...

A particle which is simultaneously subjected to two perpendicular simple harmonic motions are represented by: x=a1cos⁡ωtx={{a}_{1}}\cos \omega t and y=a2cos⁡2ωty={{a}_{2}}\cos 2\omega t traces a curve given by,
a)

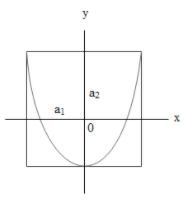
b)

c)

d)

Explanation

Solution

In the question it is given to us how the particle executes S.H.M along the x-axis and they-axis. Basically we are asked to find the path or the curve traced by the particle performing SHM along both the perpendicular axes. Hence we will obtain the relation between x and the y and accordingly determine the curve traced by the particle.

Complete answer:
It is given to us that particle is simultaneously subjected to two perpendicular simple harmonic motions which are represented by: x=a1cos⁡ωtx={{a}_{1}}\cos \omega t and y=a2cos⁡2ωty={{a}_{2}}\cos 2\omega t. Our basic aim is to determine the relation between x and y.
As per the trigonometric identity,
Cos2θ=2Cos2θ−1Cos2\theta =2Co{{s}^{2}}\theta -1
Hence using this identity in the equation of motion of the particle along y we get,
y=a2cos⁡2ωt ⇒y=a2(2cos⁡2ωt−1), ∵xa1=cos⁡ωt ⇒y=a2(2(xa1)2−1) ⇒y=2a2((xa1)2−12) \begin{aligned} & y={{a}_{2}}\cos 2\omega t \\\ & \Rightarrow y={{a}_{2}}(2{{\cos }^{2}}\omega t-1)\text{, }\because \dfrac{x}{{{a}_{1}}}=\cos \omega t \\\ & \Rightarrow y={{a}_{2}}(2{{\left( \dfrac{x}{{{a}_{1}}} \right)}^{2}}-1) \\\ & \Rightarrow y=2{{a}_{2}}\left( {{\left( \dfrac{x}{{{a}_{1}}} \right)}^{2}}-\dfrac{1}{2} \right) \\\ \end{aligned}
If we consider the above equation it represents the equation of a parabola which is facing upwards.

Hence we can say that the correct answer of the above question is option a.

Note:
In the above question we obtained the equation of the parabola. This can basically be understood by the power of the of x which is 2. Therefore we can say that the equation is a quadratic equation. If x or y both are expressed raised to some power of each other where power is equal to 2 then we can say that the curve basically represents a parabola. It is also to be noted that we need to know the different equations of parabola, when placed differently about its fixed point in order to determine the position of the curve.