Question

A particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity$\sqrt{3gr}$at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is?

A. 4:3
B. 5:4
C. 1:4
D. 3:2
E. 1:2

Answer 1

Hint:
Concepts of basic kinematics are used to solve this question. Multiple diagrams need to be made here to understand the cases easily. Force body diagrams will also be required since tension needs to be found out.

Step by step solution:

We will start off by making a simple diagram representing the vertical circular motion. Position A denotes the topmost or the highest point in the motion, while point B denotes the lowest point in the motion.

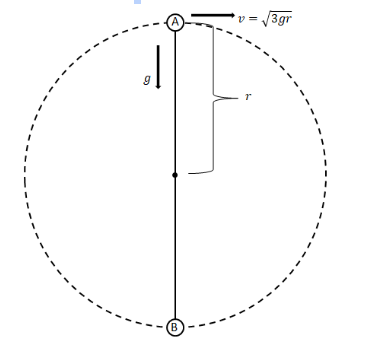
We know that potential energy $P.E=mgh$ and kinetic energy $K.E=\dfrac{1}{2}m{{v}^{2}}.$

Since at any point in the circular motion observed by the bob, total energy will be conserved, we will use this observation to find velocity at the point b${{v}_{b}}.$

Total energy of particle at point A = Total energy of the particle at point B

(K.E+P.E)(A) = (K.E+P.E)(B)
$(mg{{h}_{A}})+(\dfrac{1}{2}mv_{A}^{2})=(mg{{h}_{B}})+(\dfrac{1}{2}mv_{B}^{2})$

Substituting the values ${{h}_{A}}=2r,{{v}_{A}}=\sqrt{3gr} , {{h}_{B}}=0$ in the above equation we get,

$(mg)\centerdot 2r+\dfrac{1}{2}m{{(\sqrt{3gr})}^{2}}=(mg)\centerdot 0+(\dfrac{1}{2}mv_{B}^{2})$
$\dfrac{7}{2}mgr=\dfrac{1}{2}mv_{B}^{2}$
$7gr=v_{B}^{2}$
$\sqrt{7gr}={{v}_{B}},$

this is the velocity of the bob at the bottom of the vertical circular motion.

We will now draw a force body diagram for the bob at position A.

The 3 forces acting on the body at position A are $\dfrac{mv_{A}^{2}}{r}$ acting upward or outward, weight of the bob ($mg$) acting downward and the tension (${{T}_{A}}$) the cord pulling the bob towards itself.

The summation of all the forces acting along a single axis will be zero. Here, since all the forces are along a single axis itself, therefore, sum of all the 3 forces = 0.

$\dfrac{mv_{A}^{2}}{r}-mg-{{T}_{A}}=0$
$\dfrac{m{{(\sqrt{3gr})}^{2}}}{r}-mg-{{T}_{A}}=0$
$3mg-mg-{{T}_{A}}=0$

$2mg={{T}_{A}},$

This is the tension acting on the string at point A (the topmost point in the circular motion).

We will now draw a force body diagram for the bob at position B.

The similar 3 forces as above are acted upon the body over here as well. $\dfrac{mv_{B}^{2}}{r}$ acting downward or outward, weight of the bob ($mg$) acting downward and the tension (${{T}_{B}}$) on the cord pulling the bob towards itself.

Using the same explanation as in the previous case, the sum of all 3 forces = 0.

${{T}_{B}}-\dfrac{mv_{B}^{2}}{r}-mg=0$
${{T}_{B}}-\dfrac{m{{(\sqrt{7gr})}^{2}}}{r}-mg=0$
${{T}_{B}}-7mg-mg=0$

${{T}_{B}}=8mg,$
This is the tension acting on the string at point B (the lowest point in the circular motion).

Therefore, the required ratio of ${{T}_{A}}:{{T}_{B}}=2:8=1:4.$

Note:
The value of ${{v}_{B}}$ is greater than${{v}_{A}},$ this is necessary to get since, the kinetic energy of the bob will be greater near the bottom of the motion and similarly the potential energy of the particle will be highest at the topmost point of the circular motion.
Making the correct force body diagram with the corresponding forces and tensions along the correct directions is very critically important.