Question

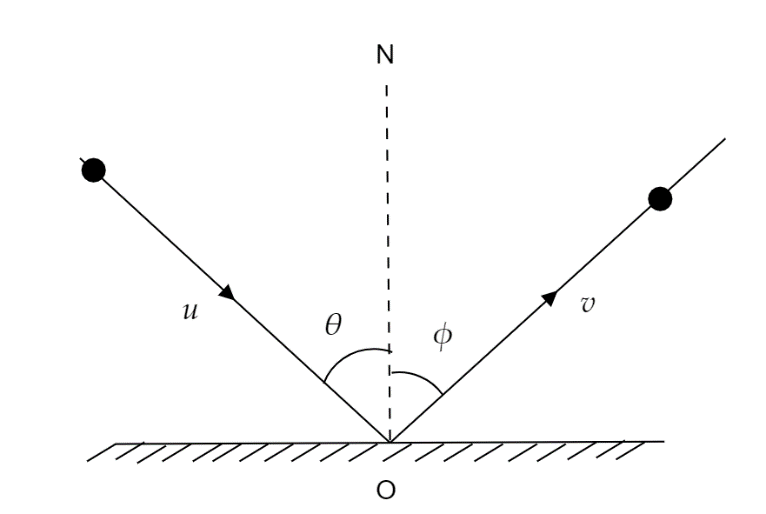
A particle strikes a horizontal frictionless floor with a speed $u$ at angle $\theta$ with the vertical, and rebounds with a speed $v$ at angle $\phi$ with the vertical. The coefficient of restitution between the particle and floor is $e$ . The magnitude of $v$ is

A. $eu$
B. $\left( {1 - e} \right)u$
C. $u\sqrt {{e^2}{{\sin }^2}\theta + {{\cos }^2}\theta }$
D. $u\sqrt {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta }$

Answer 1

In this given question, we have to use the concept of conservation of momentum to formulate the first equation. Then by applying the formula of the coefficient of restitution we will find another equation. Hence, by solving the two formulas we will find the answer.

Complete answer:
In the given question it is mentioned that the floor is frictionless. The initial velocity of the particle when it strikes the floor is $u$ and the angle at which it strikes the floor is $\theta$ in the vertical direction.
The particle again rebounds with the final velocity $v$ at angle $\phi$ in the vertical direction.
From the momentum of conservation we get,
$mu\sin \theta = mv\sin \phi$
By arranging the equation and dividing it by $m$ we get,
Or, $v\sin \phi = u\sin \theta - - - - - \left( 1 \right)$
Again, from the coefficient of restitution $e$ in the vertical direction, we get,
$\dfrac{{v\cos \phi }}{{u\cos \theta }} = e$
Or, $v\cos \phi = eu\cos \theta - - - - - \left( 2 \right)$
Now, by squaring and adding equation $\left( 1 \right)$ and equation $\left( 2 \right)$ we get,
${v^2}{\sin ^2}\phi + {v^2}{\cos ^2}\phi = {u^2}{\sin ^2}\theta + {e^2}{u^2}{\cos ^2}\theta$
Taking ${v^2}$ common in the left hand side and ${u^2}$ from the right hand side of the equation, we get,
${v^2}\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right) = {u^2}\left( {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } \right)$
From trigonometric identity we know that, ${\sin ^2}\theta + {\cos ^2}\theta = 1$
Substituting its value we get,
${v^2} = {u^2}\left( {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } \right)$
From the square root of both sides we get,
$v = \sqrt {{u^2}\left( {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } \right)} = u\sqrt {\left( {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } \right)}$
So, the magnitude of $v$ is $u\sqrt {\left( {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } \right)}$ .
The correct option is D. $u\sqrt {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta }$ .

Note:
It must be noted that we have formulated the equation of momentum conservation using sine angle as the question provided information about the vertical component only. The coefficient of restitution is the ratio of the final relative speed to the initial relative speed between two objects after their collision.