Question
Question: A particle starts from the point \(\left( {0m,8m} \right)\)and moves with uniform velocity of 3.\(\v...
A particle starts from the point (0m,8m)and moves with uniform velocity of 3.i m/s.. After 5 seconds, angular velocity of the particle about the origin will be
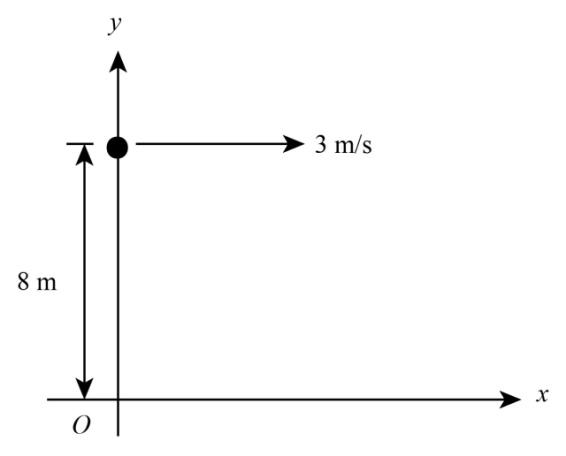
A. 2898rad/s
B. 83rad/s
C. 28924rad/s
D. 178rad/s
Solution
To solve this problem first we know about linear velocity and angular velocity. Linear velocity means the rate of change of the position of an object that is traveling along a straight line and angular velocity is defined as the rate of change of angular position of a rotating body. Also, i^ here represents the direction along the x-axis.
Complete step by step answer:
According to the given figure:
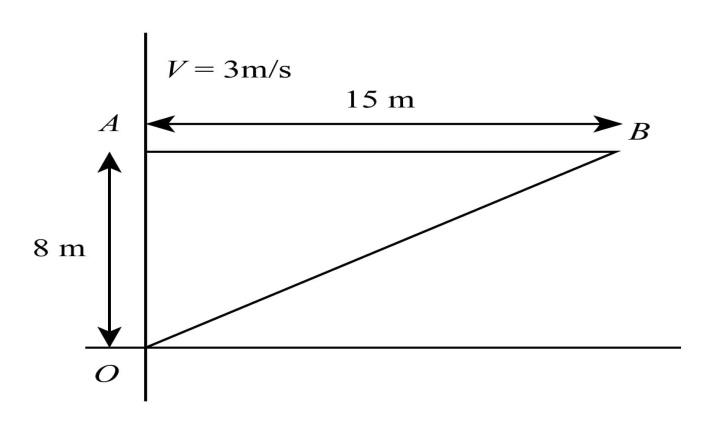
After 5seconds, the particle is at point B and has travelled a linear distance
x=v×t
x=5×3m
x=15m
Now by using Pythagoras theorem we find distance of OB
OB=82+152
OB=17m.
It is from the origin O.
Therefore, the angular velocity about the origin.
ω=v×r
(Where v is the velocity, r is the radius, ω is angular velocity.)
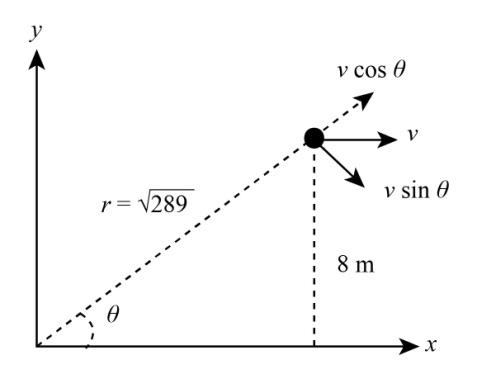
We find the value of sinθ from a right angled triangle shown in above figure by using trigonometric ratio.
sinθ=HP
(P is the perpendicular, and H is the Hypotenuse.)
⇒sinθ=178 (By using trigonometric ratio)
When body rotate about origin then we find out angular velocity
⇒ω=rvsinθ
⇒ω=r23×8
⇒ω=17224
⇒ω=28924rad/s
∴ω=28924rad/s
Therefore, the correct option is (C).
Additional information:
An object rotating about its axis, every point on the object has the same angular velocity. Tangential velocity at any point is proportional to its distance from the axis of rotation. And the rate of change of angular velocity is also called angular acceleration.
Note:
Angular velocity plays a very important role in the rotational motion of an object. If an object showing rotational motion all particles move in a circle. The linear velocity is directly related to the angular velocity of the whole object.
