Question

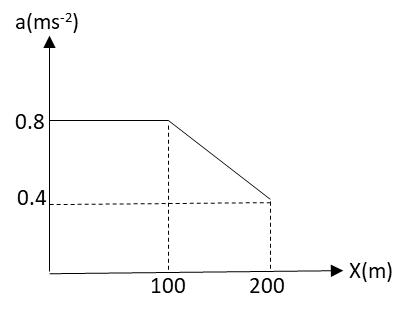
A particle starts from the origin with velocity $\sqrt {44} \,{\text{m}} \cdot {{\text{s}}^{ - 1}}$s on a straight horizontal road. Its acceleration varies with displacement as shown. The velocity of the particle as it passes through the position $x = 0.2\,{\text{km}}$ is:

A. $16\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$
B. $18\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$
C. $20\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$
D. $22\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$

Answer 1

Derive a relation between the area under the curve and velocity of the particle. Determine the area under the curve and equate it with the integration of the velocity term with respect to velocity. Integrate the velocity terms from initial velocity to the required final velocity and solve it to obtain the required velocity of the particle.

Formula used:
The acceleration $a$ of an object is
$a = \dfrac{{dv}}{{dt}}$
Here, $dv$ is the change in velocity of the object in time $dt$.
The velocity $v$ of an object is
$v = \dfrac{{dx}}{{dt}}$
Here, $dx$ is the change in displacement of the object in time $dt$.

Complete step by step solution:
We have given that a particle starts from the origin with initial velocity $\sqrt {44} \,{\text{m}} \cdot {{\text{s}}^{ - 1}}$.
We need to determine the velocity of the particle at the position $x = 0.2\,{\text{km}}$ of the particle.
The area $A$ under the acceleration-displacement curve of the particle is given by
$A = \int {adx}$
Substitute $\dfrac{{dv}}{{dt}}$ for $a$ in the above equation.
$A = \int {\dfrac{{dv}}{{dt}}dx}$
$\Rightarrow A = \int {\dfrac{{dx}}{{dx}}dv}$
Substitute $v$ for $\dfrac{{dx}}{{dx}}$ in the above equation.
$\Rightarrow A = \int {vdv}$ …… (1)
Now calculate the total area under the acceleration-displacement curve.
There are three rectangles of the same size and one triangle formed under the curve.
Hence, the area under the curve is the sum of areas of 3 rectangles and one triangle.
$\Rightarrow A = 3 \times {\text{area of rectangle}} + {\text{area of triangle}}$
$\Rightarrow A = 3 \times \left( {{\text{length}} \times {\text{breadth}}} \right) + \dfrac{1}{2}\left( {{\text{base}}} \right)\left( {{\text{height}}} \right)$
Substitute $100\,{\text{m}}$ for ${\text{length}}$, $0.4\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ for ${\text{breadth}}$, $100\,{\text{m}}$ for ${\text{base}}$ and $0.4\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ for ${\text{height}}$ in the above equation.
$\Rightarrow A = 3 \times \left( {100\,{\text{m}} \times 0.4\,{\text{m}} \cdot {{\text{s}}^{ - 2}}} \right) + \dfrac{1}{2}\left( {100\,{\text{m}}} \right)\left( {0.4\,{\text{m}} \cdot {{\text{s}}^{ - 2}}} \right)$
$\Rightarrow A = 140\,{{\text{m}}^2}$
Hence, the area under the curve is $140\,{{\text{m}}^2} \cdot {{\text{s}}^{ - 2}}$.
Now, we determine the velocity of the particle at position $x = 0.2\,{\text{km}}$.
Substitute $140\,{{\text{m}}^2} \cdot {{\text{s}}^{ - 2}}$ for $A$ in equation (1) and integrate the right hand side equation for initial velocity $\sqrt {44} \,{\text{m}} \cdot {{\text{s}}^{ - 1}}$ to the velocity $v$ at position $x = 0.2\,{\text{km}}$.
$\Rightarrow 140\,{{\text{m}}^2} \cdot {{\text{s}}^{ - 2}} = \int\limits_{\sqrt {44} \,{\text{m}} \cdot {{\text{s}}^{ - 1}}}^v {vdv}$
$\Rightarrow 140\,{{\text{m}}^2} \cdot {{\text{s}}^{ - 2}} = \left[ {\dfrac{{{v^2}}}{2}} \right]_{\sqrt {44} \,{\text{m}} \cdot {{\text{s}}^{ - 1}}}^v$
$\Rightarrow 140\,{{\text{m}}^2} \cdot {{\text{s}}^{ - 2}} = \left[ {\dfrac{{{v^2}}}{2} - \dfrac{{{{\left( {\sqrt {44} \,{\text{m}} \cdot {{\text{s}}^{ - 1}}} \right)}^2}}}{2}} \right]$
$\Rightarrow 140 = \left[ {\dfrac{{{v^2}}}{2} - 22} \right]$
$\Rightarrow {v^2} = 2\left( {140 + 22} \right)$
$\Rightarrow {v^2} = 2\left( {162} \right)$
$\Rightarrow {v^2} = 324$
$\Rightarrow v = 18\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$
Therefore, the required velocity of the particle is $18\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$.

So, the correct answer is “Option B”.

Note:
The students may think that the area under the curve obtained does not have the unit of area which is meter square. But students should keep in mind that we have just mentioned the terms as area (as it is the area under the curve) but the area under the acceleration-displacement curve actually gives the kinetic energy per unit mass of the particle.