Question

A particle starts from rest at x = 0 and its acceleration varies with x as shown in figure. Then

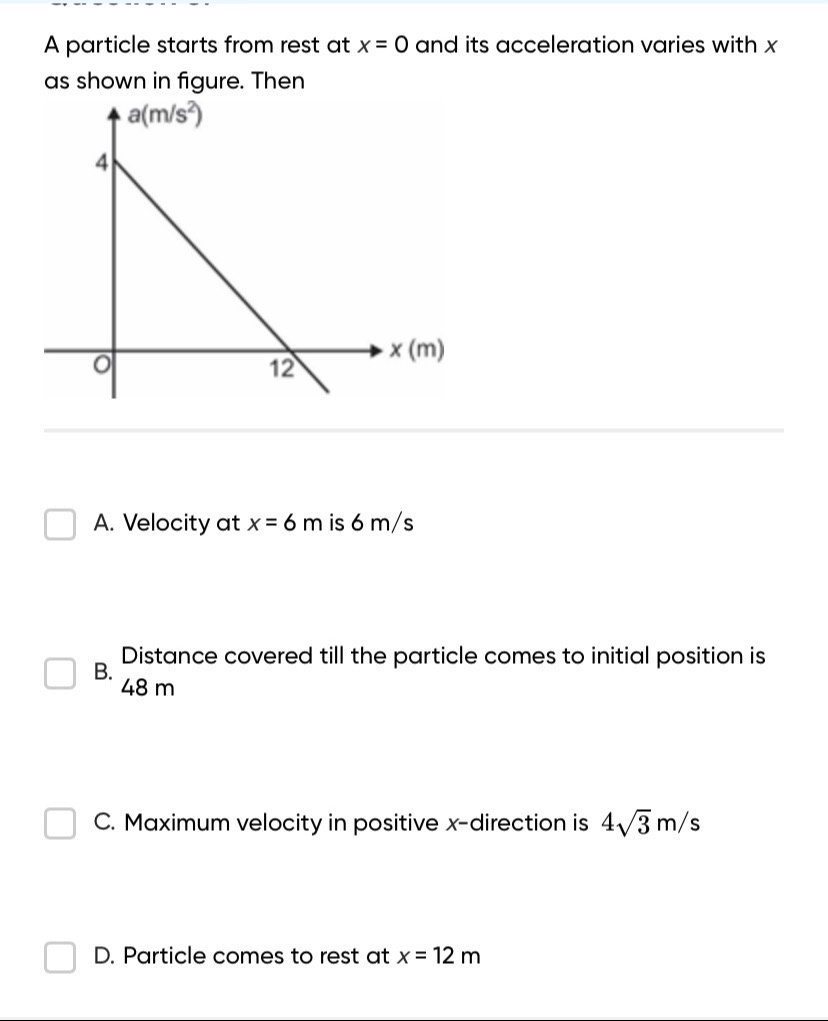
• A. Velocity at x = 6 m is 6 m/s
• B. Distance covered till the particle comes to initial position is 48 m
• C. Maximum velocity in positive x-direction is 4$\sqrt{3}$ m/s
• D. Particle comes to rest at x = 12 m

Answer 1

Answer: (A), (C)

A and C

Answer 2

The acceleration is given by $a(x) = -\frac{1}{3}x + 4$. Using $v \, dv = a \, dx$, we integrate to find $v^2 = -\frac{x^2}{3} + 8x$. The motion is restricted to $0 \le x \le 24$. Option A: At $x=6$, $v^2 = -\frac{6^2}{3} + 8(6) = -12 + 48 = 36$, so $v=6$ m/s. Option C: Maximum velocity occurs when $a=0$, which is at $x=12$. At $x=12$, $v^2 = -\frac{12^2}{3} + 8(12) = -48 + 96 = 48$, so $v=4\sqrt{3}$ m/s. Option B: The particle stops at $x=24$ m and does not return to $x=0$. The distance covered is 24 m. Option D: The particle stops at $x=24$ m, not $x=12$ m.