Question

A particle starts from origin and moving along $x-$ axis, whose $v-t$ graph is as shown. Choose the Incorrect statement

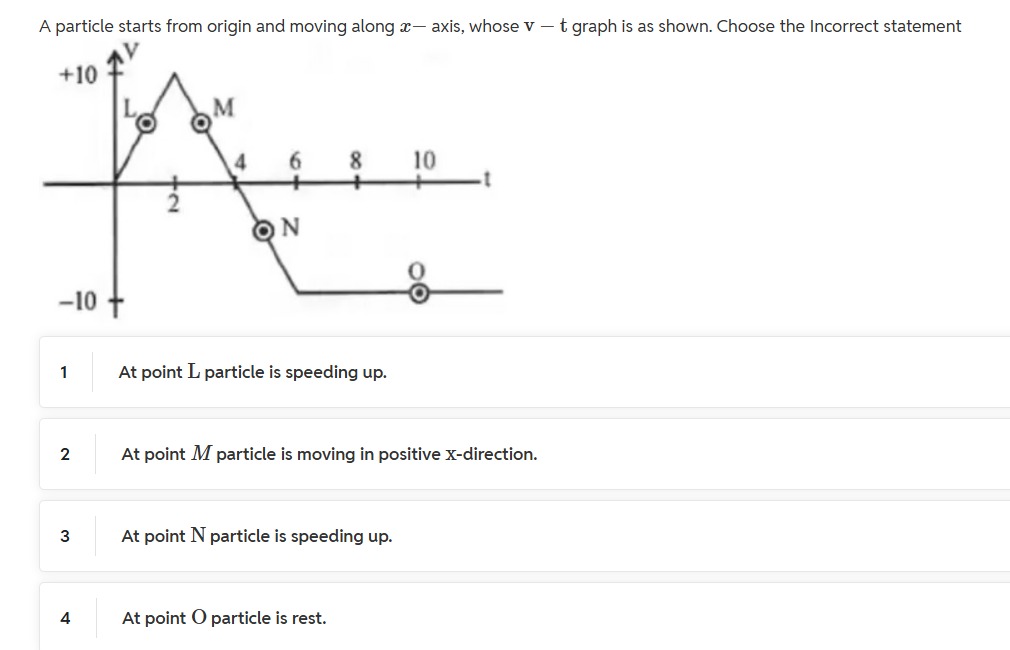
• A. At point $L$ particle is speeding up.
• B. At point $M$ particle is moving in positive $x$-direction.
• C. At point $N$ particle is speeding up.
• D. At point $O$ particle is rest.

Answer 1

Answer: (D)

At point $O$ particle is rest.

Answer 2

The solution involves analyzing the given velocity-time ($v-t$) graph to determine the motion of the particle at specific points.

• Speeding up: A particle is speeding up if its speed (magnitude of velocity, $|v|$) is increasing. This occurs when the velocity ($v$) and acceleration ($a$) have the same sign. From a $v-t$ graph, acceleration is the slope of the graph.
• Direction of motion: The sign of the velocity indicates the direction of motion. Positive velocity means motion in the positive $x$-direction, and negative velocity means motion in the negative $x$-direction.
• Rest: A particle is at rest when its velocity is zero ($v=0$).

Let's analyze each statement:

1. At point $L$ particle is speeding up. Point $L$ is at $t=1$. From the graph, at $t=1$, the velocity $v$ is positive and increasing. The slope of the $v-t$ graph at $L$ is positive, indicating positive acceleration. Since both $v$ and $a$ are positive, the particle is speeding up. This statement is correct.

2. At point $M$ particle is moving in positive $x$-direction. Point $M$ is at $t=3$. From the graph, at $t=3$, the velocity $v$ is positive. A positive velocity means the particle is moving in the positive $x$-direction. This statement is correct.

3. At point $N$ particle is speeding up. Point $N$ is at $t=6$. From the graph, at $t=6$, the velocity $v$ is negative. The slope of the $v-t$ graph at $N$ is negative, indicating negative acceleration. Since both $v$ and $a$ are negative, the particle's speed is increasing. Thus, the particle is speeding up. This statement is correct.

4. At point $O$ particle is rest. Point $O$ is at $t=10$. From the graph, at $t=10$, the velocity $v$ is $-10$. For the particle to be at rest, its velocity must be zero. Since $v = -10 \neq 0$, the particle is not at rest. This statement is incorrect.

Since the question asks for the incorrect statement, option 4 is the answer.