Question

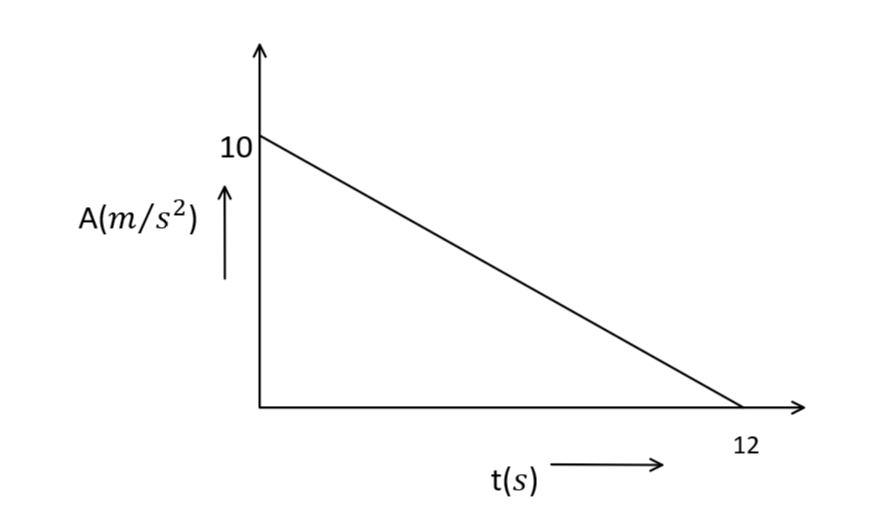
A particle starting from rest undergoes a rectilinear motion with acceleration$a$. The variation of $a$with time is shown below. The maximum velocity attained by the particle during its motion is

A) $120\,m$/$s$
B) $60\,m$/$s$
C) $22\,m$/$s$
D) $80\,m$/$s$

Answer 1

In this question, we have to find the maximum velocity during the rectilinear motion with acceleration$a$. For that we have to find the area under the curve where acceleration $a$has the maximum value

Complete step by step answer:

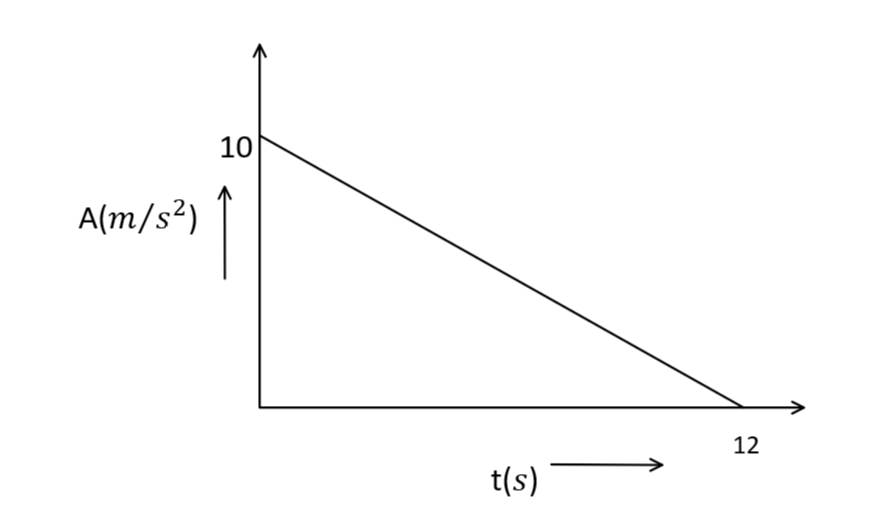
In this question, we have to find the maximum velocity during the rectilinear motion with acceleration ($a$)
Since, we know that
$a = \dfrac{{dv}}{{dt}}$
Or we can write the above equation as,
$v = \int {a.dt}$
Therefore, for finding the maximum velocity we have to find the area under the curve where $a$is maximum
As we can see in the graph the maximum value of a is $10\,m$/$s$
Now, since the graph is in the form of triangle, area under the curve will be, $\dfrac{1}{2} \times X - axis\, \times \,Y - axis$
On putting the values we get,
$\dfrac{1}{2} \times 10\, \times \,12 = 60$

Hence, the maximum velocity during the rectilinear motion with acceleration ($a$) will be $60\,m$/${s^2}$

Note: For this type of question, the best method to solve is to find the area under the curve for the required intervals by integration or else we can do it by the normal method as we did in the above question.