Question

A particle revolves around a circular path with a uniform speed. The centripetal acceleration of the particle is:
A) Along the circumference of the circle
B) Along the tangent
C) Along the radius
D) Zero

Answer 1

According to question, we need to find the direction of centripetal acceleration of the particle revolving around a circular path with uniform speed. The acceleration due to the particle moving in a circular path is of two types-tangential acceleration and centripetal acceleration. Centripetal means towards the centre. Centripetal force is responsible for bending the straight path of an object to a circular path and Tangential acceleration always directed towards the tangent to the path of the body.

Complete answer:
Centripetal acceleration: is defined as the property of the motion of an object, traversing a circular path. Any object that is moving in a circle and has an acceleration vector pointed towards the centre of that circle is known as Centripetal acceleration. This can be shown in the following diagram.

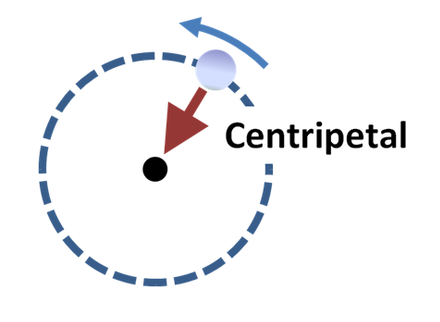
You must have seen various examples of centripetal acceleration in your everyday life. If you drive a car around a circle then your car is undergoing centripetal acceleration and a satellite orbiting the earth also follows a centripetal acceleration.
Tangential acceleration: is similar to linear acceleration, but it is specific to the tangential direction. This is related to circular motion. Therefore, the rate of change of the tangential velocity of a particle in a circular orbit is known as Tangential acceleration. It always directs towards the tangent to the path of the body. Tangential acceleration will work if an object is moving in a circular path. Tangential acceleration is like linear acceleration, but it’s different from the straight-line linear acceleration. An object is linearly accelerating if it’s travelling in a straight-line path.

In the case of tangential acceleration, the velocity of a particle changes, but in this case we can clearly see that here uniform velocity is present, the value for tangential acceleration becomes zero.Thus, we can say that the centripetal acceleration of the particle is along the circumference of the circle.
Therefore, option (A) is correct.

Note:
It should be noted that the students must know the basic difference between tangential acceleration and centripetal acceleration. Tangential acceleration is the measure of how fast a tangential velocity changes, whereas, centripetal acceleration is the acceleration which acts radially towards the centre of the circle.