Question

A particle performing a U.C.M. of radius $\pi$ m makes ‘p’ revolutions in ‘t’ seconds. What is its tangential velocity?
$A.\,\dfrac{2{{\pi }^{2}}p}{t}\,{m}/{s}\;$
$B.\,\dfrac{2{{\pi }^{2}}}{pt}\,{m}/{s}\;$
$C.\,\dfrac{{{\pi }^{2}}p}{t}\,{m}/{s}\;$
$D.\,\dfrac{2\pi p}{t}\,{m}/{s}\;$

Answer 1

The value of the tangential velocity of a particle can be found as the ratio of the circumference of the uniform circular path by the time taken by a particle to complete the revolutions. Here, instead of the displacement, we have considered the circumference of the circle, as this is a circular motion.

Formula used: $v=\dfrac{C}{t}$

Complete step by step answer:
The basic formula used to find the value of the velocity of any particle is given as follows.
$v=\dfrac{d}{t}$
Where d is the displacement and t is the time taken.
A diagram representing the direction of the velocity of a particle performing U.C.M.

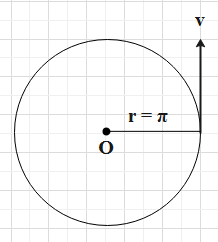
In this case, we are given with the uniform circular motion. So, the particle covers the distance equal to that of the circumference of the circular path. Thus, in the above formula, we will replace the displacement with the circumference of the circle in terms of the revolutions completed.
So, we have,
$v=\dfrac{C'}{t}$ …… (1)
This equation represents the tangential velocity of a particle performing U.C.M.
The circumference of the circle is given as follows.
$C=2\pi r$
Substitute the value of the radius from the given data. As we are given with the value of radius to be equal to $\pi$meters, so, we will substitute the same in the above equation.

& C=2\pi (\pi ) \\\ & \Rightarrow C=2{{\pi }^{2}} \\\ \end{aligned}$$ The circumference with reference to the revolutions completed is given as follows. $$C'=C\times p$$ As we are given the number of revolutions to be equal to the value of ‘p’. Substitute the value of the circumference of the circle in the above equation. $$C'=2{{\pi }^{2}}\times p$$ The time taken by the particle to cover the distance is given to be equal to ‘t’. Now substitute all these values obtained in the above equation (1) of the tangential velocity. $$v=\dfrac{2{{\pi }^{2}}p}{t}$$ As the expression for the tangential velocity of the particle performing U.C.M is $$\dfrac{2{{\pi }^{2}}p}{t}$$. **So, the correct answer is “Option A”.** **Note:** The uniform circular motion is the distance or the movement along the circular path or along the circumference of the circle covered by an object. The tangential velocity is the speed with which an object is moving in a circular path. In this case, we have derived the expression for the tangential velocity, if in case, asked to find the expression for the angular acceleration, then, simply divide the expression of velocity by time.