Question

A particle originally at rest at the highest point on a smooth vertical circle is slightly displaced. It will leave the circle at a vertical distance $h$ below the highest point such that:
(A) $h = R$
(B) $h = \dfrac{R}{3}$
(C) $h = \dfrac{R}{2}$
(D) $h = \dfrac{R}{4}$

Answer 1

Here, it is clearly given that the circle is vertical and smooth i.e. frictionless. When the particle is moving on the circle with velocity $v$ from the highest point. We have to use the resolving of forces concept and also the conservation of energy concept to find the velocity and also the height of the particle at which it leaves the circle.

Complete step by step solution:
According to the given information the particle is moving on the circle which is smooth and there is no frictional force acting on the particle. The circle is vertical and the particle is at its highest point when it moves. It comes at the point where it makes $h$ distance from the vertical point.
Let us consider the figure above and resolve the forces acting on the particle as given in the figure below:

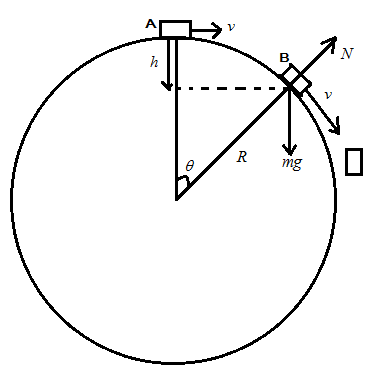
$R$ is the radius of the vertical circle, $h$ is the vertical distance from the initial position of the particle at point A to the point B at which the particle leaves the circle.
Therefore, height is given by
$h = R - R\cos \theta$ ….. $(1)$
$N$ be the normal acting on particle in contact with circle, it equates with the component opposite to normal of $mg$ is $mg\cos \theta$ and centripetal force acting on the body
Therefore, net force is given by
$mg\cos \theta - N = \dfrac{{m{v^2}}}{R}$
When, particle leaves the circle the $N$ becomes $zero$
$\Rightarrow mg\cos \theta = \dfrac{{m{v^2}}}{R}$
$\Rightarrow {m}g\cos \theta = \dfrac{{{m}{v^2}}}{R}$
$\Rightarrow {v^2} = R\cos \theta g$ ….. $(2)$
Now, by using the energy conservation law for initial and final position of particle, we get
$mgh = \dfrac{1}{2}m{v^2}$
$\Rightarrow v = \sqrt {2gh}$ ….. $(3)$
From $(2)$ and $(3)$ , we get
$\Rightarrow {\left( {\sqrt {2gh} } \right)^2} = R\cos \theta g$
$\Rightarrow 2g(R - R\cos \theta ) = R\cos \theta g$
$\Rightarrow \cos \theta = \dfrac{{2R(1 - \cos \theta )}}{R}$
$\Rightarrow \cos \theta = 2 - 2\cos \theta$
$\Rightarrow \cos \theta = \dfrac{2}{3}$
Therefore, height is given by:
$h = R - R\left( {\dfrac{2}{3}} \right)$
$\therefore h = \dfrac{R}{3}$
Hence, we reached the solution that the height at which the particle leaves the contact with circle is $\dfrac{R}{3}$
The correct answer is option (B).

Note:
We must take care while resolving the forces acting on the particle and also while using the concept of conservation of energy. At the initial stage the kinetic energy of the particle was zero and then at the final stage potential energy of the particle will be zero. Thus, we can calculate the velocity and height by using velocity.