Question

A particle of specific charge $\dfrac{q}{m}=\pi ck{{g}^{-1}}$ is projected from the origin towards $+ve\text{ }x-axis$ with a velocity of $10m{{s}^{-1}}$ in a uniform magnetic field $\overrightarrow{B}=-2\widehat{k}T$.The velocity of the particle after time $\overrightarrow{t}=\dfrac{1}{12}s$ will be..
A. $5\left[ \hat{i}+\sqrt{3}\hat{j} \right]$
B. $5\left[ \sqrt{3}\hat{i}+\hat{j} \right]$
C. $5\left[ \sqrt{3}\hat{i}-\hat{j} \right]$
D. $5\left[ \hat{i}+\hat{j} \right]$

Answer 1

Let a charged particle enter in a magnetic field (uniform) with a velocity perpendicular to the direction of field. We see that a force starts acting on the particle and revolves in a circular path.

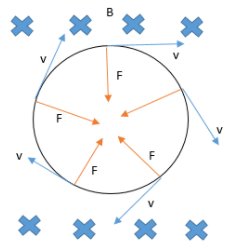
We termed 2 X magnetic fields inside the paper. In such conditions we observe that there is a particular radius of the circular path and a time period of Revolution is there.
In our diagram we conclude that a force is acting on the particle at every point which made it revolve in circular path as it is acting towards radius (centripetal force)

Complete answer:
We can write:
Centripetal force = Magnetic force.
$\dfrac{m{{v}^{2}}}{r}=qvB$
$v=\dfrac{qBr}{m}\text{ }\left( \text{This is the velocity of the particle} \right)$
$r=\dfrac{mv}{qB}$
Time period of revolution $=\dfrac{2\pi r}{v}$
$T=\dfrac{2\pi }{v}\left( \dfrac{mv}{qB} \right)$
$T=\dfrac{2\pi m}{qB}$
Let the direction of magnetic field in -z direction then if a particle with velocity ‘v’ making an angle $\theta$ with field enters into it the components of velocity are divided into $\sin$ and $\cos ine$.
According to our discussion Time period of Revolution is
$T=\dfrac{2\pi m}{qB}=\dfrac{2\pi m}{\left( \dfrac{q}{m} \right)B}\text{ }\left( \text{given }q=\dfrac{q}{m} \right)$
$T=2\pi =1s$
After a time period of $\dfrac{1}{12}\sec ,\theta =\dfrac{360{}^\circ }{12}=30{}^\circ$
The velocity components are
$\overrightarrow{v}=10\left( \cos 30\widehat{i}+\sin 30\widehat{j} \right)$
$\overrightarrow{v}=10\left( \dfrac{\sqrt{3}}{2}\widehat{i}+\dfrac{1}{2}\widehat{j} \right)$
$\overrightarrow{v}=5\left( \sqrt{3}\widehat{i}+\widehat{j} \right)$

The correct answer is option B.

Note:
The velocity component if perpendicular to the magnetic field then the particle is revolved in a circular path. As we have discussed that this path has its own velocity and revolution time - Let the particle enter parallel to the field. In this case the particle moves parallel with the same velocity in the direction of the field. We have a charged particle with motion having angle $'\theta '$ with the field then the particle moves in helical motion.