Question
Question: A particle of sass 20g is released with an initial velocity \[5{\text{ m/s}}\] along the curve from ...
A particle of sass 20g is released with an initial velocity 5 m/s along the curve from point A, as shown in the figure. The point A is at length h from B. The particle slides along the frictionless surface. When the particle reaches point B, its angular momentum O will be: (Take g=10 ms−2)
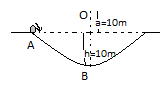
A) 2 kg - m2s−1
B) 8 kg - m2s−1
C) 3 kg - m2s−1
D) 6 kg - m2s−1
Solution
In this question, we need to determine the angular momentum of particle B when it reaches at point B. For this we will use the relation as L=r×p, where
L is the angular momentum of a moving particle about a point
r is the length of perpendicular on the line of motion
p is the component of momentum along the perpendicular to r
Complete step by step answer:
Mass of the particle m=20g
The velocity of the particle at point a is Va=5 m/s
Since the velocity of the particle will be different for two points, hence we apply work-energy theorem from point A to B
Wf=△KE−−(i)
For two points equation (i) can be written as
mgh=21mvB2−21mvA2−−(ii)
Equation (ii) can be further written as
Now by substitute the values of vAandh, we get
2gh=vB2−vA2 ⇒2×10×10=vB2−(5)2 ⇒vB2−25=200 ⇒vB2=225 ⇒vB=15 m/sHence the angular momentum about O will be
L=mvrOB =100015×15×20 =6 kg - m2s−1Option D is correct.
Note: Angular momentum is the same as linear momentum, but it is in rotational form. Angular momentum is a vector quantity, and it is the product of a body's rotational inertia and rotational velocity about a particular axis.
