Question

A particle of mass $m$ was transferred from the centre of the base of a uniform hemisphere of mass $M$ and radius $R$ into infinity. What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?

Answer 1

- Hint: The idea is to consider a small hemispherical cross-section of thickness $dr$ at a radius $r$ from the centre of the base of the hemisphere, inside the hemisphere. We find the gravitational potential due to this section at the centre of the base of the hemisphere to calculate the net gravitational potential at the same point due to the total mass $M$ of the hemisphere. The corresponding value of gravitational potential when a particle of mass $m$ is placed at the centre of the base of the hemisphere is found out. The work done by the gravitational force to separate these masses infinitely is equal to this gravitational potential.

Formula used:
$1)\phi =-\dfrac{Gm}{r}$
where
$\phi$ is the gravitational potential due to a particle of mass $m$at a distance $r$
$G$ is the gravitational constant
$2)\rho =\dfrac{dM}{dV}\Rightarrow \dfrac{M}{V}=\dfrac{dM}{dV}\Rightarrow dM=\left( \dfrac{M}{V} \right)dV$
where
$\rho$ is the density of the volume $(V)$-mass $(M)$ density of the hemisphere
$dM$ and $dV$ are the mass and volume of a small section of hemisphere
$3)V=\dfrac{2}{3}\pi {{R}^{3}}$
where
$V$ is the volume of the hemisphere
$R$ is the radius of the hemisphere
$4)dV=\dfrac{4\pi {{R}^{2}}}{2}=2\pi {{R}^{2}}$
where
$dV$ is the volume of a cross-section of hemisphere
$R$ is the radius of the hemisphere
$4\pi {{R}^{2}}$ is the volume of a small cross-sectional sphere, considered inside the sphere
$4)W=m\phi$
where
$m$ is the mass of a particle at the centre of the base of the hemisphere
$\phi$ is the gravitational potential at the centre of the base of the hemisphere
$W$ is the work done to separate a particle of mass $m$ from the centre of the base of the hemisphere to infinity.

Complete step-by-step solution
We have a hemisphere whose mass is $M$ and radius is $R$. A particle of mass $m$ is kept at the centre of the base of the hemisphere. This particle is separated to infinity with the help of gravitational force acting on the particle by the hemisphere. What we require to calculate is the work done by gravitational force to separate the particle to infinity from the base of the centre of the hemisphere.
Work done by gravitational force is equal to the gravitational potential acting on a particle. Therefore, to calculate the work done to separate the particle to infinity, it is enough to calculate the gravitational potential acting on the particle of mass $m$ due to the hemisphere of mass $M$.
The gravitational potential at a distance $r$ due to a mass $m$ is given by
$\phi =-\dfrac{Gm}{r}$, where $G$ is the gravitational constant.
To obtain the gravitational potential due to the hemisphere on the particle, firstly, let us consider a small cross-section of hemisphere of thickness $dr$ and mass $dM$ at a distance $r$ from the centre of the base of the hemisphere, inside the hemisphere (as shown in the figure). We determine the gravitational potential at the centre of the base of the hemisphere due to this cross-section and then, we integrate it over $R$ to get the gravitational potential at the centre due to the whole hemisphere.

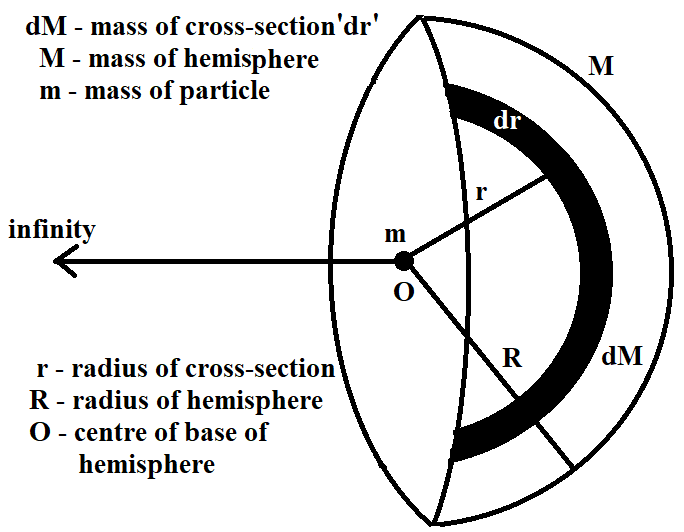
Gravitational potential due to the small cross-section of hemisphere is given by
$d\phi =-\dfrac{GdM}{r}$
where
$dM$is the mass of the small cross-sectional hemisphere at a distance $r$ from the centre of the base of the hemisphere. Let this be equation 1.
$dM$ is given by
$dM=\rho dV=\left( \dfrac{M}{V} \right)dV$
where
$\rho$ is the density of the hemisphere
$M$ is the mass of the hemisphere
$V$ is the volume of the hemisphere
$dM$ is the mass of the cross-sectional hemisphere
$dV$ is the volume of the cross-sectional hemisphere
Let this be equation 2.
We know that volume of a hemisphere is given by
$V=\dfrac{2}{3}\pi {{R}^{3}}$
where $R$ is the radius of the hemisphere.
We also know that
$dV=\dfrac{4\pi {{R}^{2}}}{2}=2\pi {{R}^{2}}$
where
$dV$ is the volume of the cross-sectional hemisphere
$4\pi {{R}^{2}}$ is the volume of a small cross-sectional sphere, considered inside the sphere, as shown in the figure.

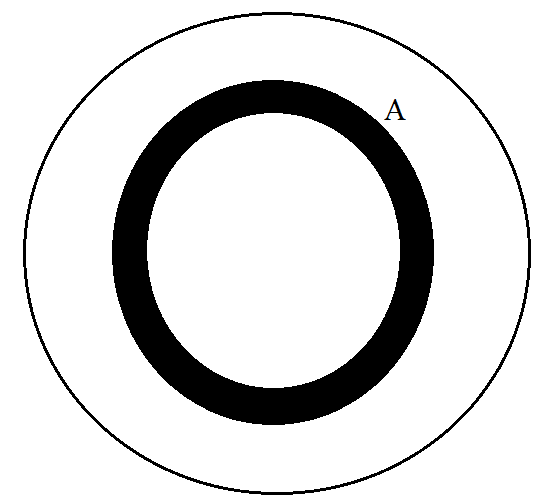
Here, $A=4\pi {{R}^{2}}$
Substituting these values in equation 2, we have
$dM=\left( \dfrac{M}{V} \right)dV=\left( \dfrac{M}{\dfrac{2}{3}\pi {{R}^{3}}} \right)2\pi {{r}^{2}}=\dfrac{3M{{r}^{2}}}{{{R}^{3}}}$
Let this be equation 3.
Substituting this value in equation 1, we have
$d\phi =-\dfrac{GdM}{r}=-\dfrac{G\dfrac{3M{{r}^{2}}}{{{R}^{3}}}}{r}=-\dfrac{3GMr}{{{R}^{3}}}$
Here, $d\phi$ is the gravitational potential by a small cross-sectional area of thickness $dr$at the centre of the base of the hemisphere.
Now, let us integrate this value from $0\to R$ to get the gravitational potential due to the hemisphere at the centre of the base of the hemisphere.
$\phi =\int\limits_{0}^{R}{d\phi }=\int_{0}^{R}{-\dfrac{3GMrdr}{{{R}^{3}}}}=-\dfrac{3GM}{{{R}^{3}}}\int\limits_{0}^{R}{rdr}=-\dfrac{3GM}{2R}$
Finally, the work done by the gravitational force to separate a particle of mass $m$ from the centre of the base of a hemisphere of mass $M$ to infinity $(0\to \infty )$ is given by
$W=m\phi =-\dfrac{3GMm}{2R}$
Therefore, the answer is
$W=-\dfrac{3GMm}{2R}$

Note: It is important to note that the final answer is a negative value. This means that the work done by the gravitational force to separate a particle from the centre point of a hemisphere is negative. This case is similar to the work done by the gravitational force when we jump. The gravitational force exerts force in the downward direction, but we move in the upward direction. Both force and displacement are in opposite directions. Hence, the work done is negative.