Question

A particle of mass m moving towards west with speed v collides with another particle of mass m moving towards south. If two particles stick to each other the speed of the new particle of mass 2 m will be
A. $v\sqrt{2}$
B. $\dfrac{v}{\sqrt{2}}$
C. $\dfrac{v}{2}$
D. $v$

Answer 1

Initially, we have to understand this question by establishing vector form for the directions. By using the conservation of linear momentum which states that momentum for a given body remains constant. i.e., momentum can neither be created nor be destroyed we will be able to find the final velocity of the particle formed after collision.

Complete Step-By-Step answer:
We will start by allocating unit vectors to each direction. Taking the east direction to be $\hat{i}$, then the west direction will be $-\hat{i}$. Now taking the north to be $\hat{j}$, the south will be $-\hat{j}$.

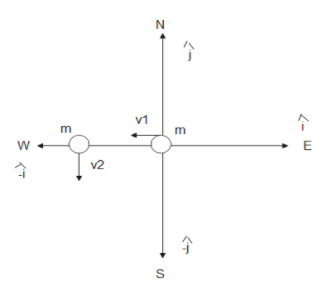
Moreover, we have been given that particle 1 of mass m is moving towards the west. Let us take the velocity of this particle to be ${{v}_{1}}$.
i.e., ${{m}_{1}}=m$ and ${{v}_{1}}=-v\hat{i}$
Where, $-\hat{i}$ denotes the direction of the velocity of particle 1.

We have particle 2 of mass m which is moving towards the south. Let us take the velocity of this particle to be ${{v}_{2}}$.
i.e., ${{m}_{2}}=m$ and ${{v}_{2}}=-v\hat{j}$
Where, $-\hat{j}$ denotes the direction of velocity of particle 2.

Now when particle 1 and particle 2 collide, they stick together having a mass of 2m. let the velocity of this new particle be taken as ${{v}_{3}}$. But the velocity of this particle be represented in the vector form $\vec{v}$. Now let us resolve $\vec{v}$ into x and y components, we get, ${{\vec{v}}_{x}}$and ${{\vec{v}}_{y}}$.

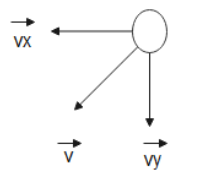
Now we will apply conservation of linear momentum in the x-direction, we get,
$\Rightarrow {{v}_{x}}= {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}=({{m}_{1}}+{{m}_{2}})\times {{v}_{3}}$
We have,
${{m}_{1}}=m$
${{v}_{1}}=-v\hat{i}$
${{m}_{2}}=m$
${{v}_{2}}=(0)\hat{i}$……………, (as for the x component)

Now, we will substitute the values we get,

&\Rightarrow m(-v)\hat{i}+m(0)\hat{j}=(2m)\times {{v}_{3}} \\\ &\Rightarrow {{v}_{x}}={{v}_{3}}=-\dfrac{v}{2}\hat{i} \\\ \end{aligned}$$ Now, we will apply conservation of linear momentum in the y-direction, we get, $\Rightarrow {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}=({{m}_{1}}+{{m}_{2}})\times {{v}_{3}}$ We have, $${{m}_{1}}=m$$ $${{v}_{1}}=(0)\hat{j}$$………., (as for y component) $${{m}_{2}}=m$$ $${{v}_{2}}=-v\hat{j}$$ We will substitute the values in the above equation, we get, $\Rightarrow m(0)\hat{j}+m(-v)\hat{j}=(2m)\times {{v}_{3}}$ $\Rightarrow {{v}_{y}}={{v}_{3}}=-\dfrac{v}{2}\hat{j}$ Now, let us take the final velocity of the particle formed due to collision as $${{v}_{0}}$$. $\Rightarrow {{v}_{0}}=\sqrt{{{({{v}_{x}})}^{2}}+{{({{v}_{y}})}^{2}}}$, we will be using this formula to find the final velocity Now substituting the values, we get, $\Rightarrow {{v}_{0}}=\sqrt{{{\left( -\dfrac{v}{2} \right)}^{2}}+{{\left( -\dfrac{v}{2} \right)}^{2}}}$ $$\begin{aligned} &\Rightarrow {{v}_{0}}=\sqrt{\dfrac{{{v}^{2}}}{4}+\dfrac{{{v}^{2}}}{4}}=v\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=v\sqrt{\dfrac{1}{2}} \\\ &\Rightarrow {{v}_{0}}=\dfrac{v}{\sqrt{2}} \\\ \end{aligned}$$ **Hence, option B is the correct answer.** **Note:** It is to be noted that the law of conservation of momentum states that momentum of a given body remains constant implying that momentum can neither be created nor be destroyed. Students need to be observative while substituting the values as any mistake in substitution will result in wrong answers.