Question
Question: A particle of mass \(m\) moves with the potential energy \(U\) as shown below. The period of the mot...
A particle of mass m moves with the potential energy U as shown below. The period of the motion when the particle has total energy E is:
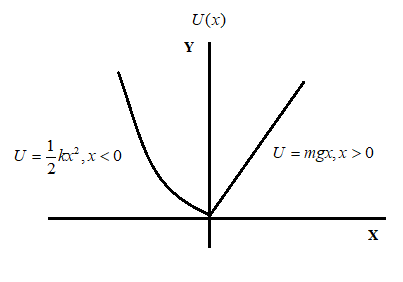
A. 2πkm+4mg22E
B. 2πkm
C. πkm+2mg22E
D. 2mg22E
Solution
Here, we have a particle whose potential energy graph is given to us. From the graph we can see that the potential energy of the graph varies with respect to the negative and positive of the x axis. Thus to find the total energy, we must calculate the energy of the sides individually and then add them up.
Formula used:
F=−dxdU
Complete answer:
Let's assume that the time period of the motion be T and the total energy be E.
Let us first look at the negative x-axis. Here the potential energy U(x)=21kx2. Now the time taken by the particle is given as Tl
The force F on the left side is given as F=−dxdU
⟹F=−22kx
⟹F=−kx
We also know that F=ma
Then we have ma=−kx
⟹a=−mkx
Clearly, the left side motion of the particle is SHM, since a∝(–x)
Then comparing a=−ω2x to the above equation, we get ω2=mk
⟹ω=mk
Since this occurs during time period T, we get,
⟹T2π=mk
⟹T=2πkm
Since SHM is a to-and-fro motion, we can say that, Tl=2T=πkm
Similarly, now consider the right side of the graph, we have U(x)=mgx
The force F on the left side is given as F=−dxdU
⟹F=−mg
⟹a∝–g
If u is the velocity of the particle, then the kinetic energy of the particle is given as KE=21mu2
Then the total energy of the particle on the right side is given as E=KE=21mu2
⟹u=2Em
Then the time taken by the particle along the right side is given as v’=u−gt, when v’ is zero, we have ,
⟹u=gt
⟹t=gu
⟹t=g2Em
Then, considering the to-and-fro motion Tr=g22Em
Then the total time take T is given as T=Tl+Tr
⟹T=πkm+g22Em
Thus the correct answer is option C. πkm+2mg22E
Note:
To solve this sum we must note the following:
The left side and the negative side of the graph have different potential energy and hence different acceleration and time period. When considering the time period of any particular side, we must also account for the too and for motion of the particle.
